concept of travelling salesman problem

Data Structures
Linked List
Binary Tree
Binary Search Tree
Segment Tree
Disjoint Set Union
Fenwick Tree
Red-Black Tree
Advanced Data Structures
Graph Data Structure And Algorithms
Introduction to Graphs - Data Structure and Algorithm Tutorials
Graph and its representations
Types of Graphs with Examples
Basic Properties of a Graph
Applications, Advantages and Disadvantages of Graph
Transpose graph
Difference Between Graph and Tree

BFS and DFS on Graph

Breadth First Search or BFS for a Graph
Depth First Search or DFS for a Graph
Applications, Advantages and Disadvantages of Depth First Search (DFS)
Applications, Advantages and Disadvantages of Breadth First Search (BFS)
Iterative Depth First Traversal of Graph
BFS for Disconnected Graph
Transitive Closure of a Graph using DFS
Difference between BFS and DFS

Cycle in a Graph

Detect Cycle in a Directed Graph
Detect cycle in an undirected graph
Detect Cycle in a directed graph using colors
Detect a negative cycle in a Graph | (Bellman Ford)
Cycles of length n in an undirected and connected graph
Detecting negative cycle using Floyd Warshall
Clone a Directed Acyclic Graph

Shortest Paths in Graph

How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
Bellman–Ford Algorithm
Floyd Warshall Algorithm
Johnson's algorithm for All-pairs shortest paths
Shortest Path in Directed Acyclic Graph
Multistage Graph (Shortest Path)
Shortest path in an unweighted graph
Karp's minimum mean (or average) weight cycle algorithm
0-1 BFS (Shortest Path in a Binary Weight Graph)
Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

Kruskal’s Minimum Spanning Tree (MST) Algorithm
Difference between Prim's and Kruskal's algorithm for MST
Applications of Minimum Spanning Tree
Total number of Spanning Trees in a Graph
Minimum Product Spanning Tree
Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

Topological Sorting
All Topological Sorts of a Directed Acyclic Graph
Kahn's algorithm for Topological Sorting
Maximum edges that can be added to DAG so that it remains DAG
Longest Path in a Directed Acyclic Graph
Topological Sort of a graph using departure time of vertex

Connectivity of Graph

Articulation Points (or Cut Vertices) in a Graph
Biconnected Components
Bridges in a graph
Eulerian path and circuit for undirected graph
Fleury's Algorithm for printing Eulerian Path or Circuit
Strongly Connected Components
Count all possible walks from a source to a destination with exactly k edges
Euler Circuit in a Directed Graph
Word Ladder (Length of shortest chain to reach a target word)
Find if an array of strings can be chained to form a circle | Set 1
Tarjan's Algorithm to find Strongly Connected Components
Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

Max Flow Problem Introduction
Ford-Fulkerson Algorithm for Maximum Flow Problem
Find maximum number of edge disjoint paths between two vertices
Find minimum s-t cut in a flow network
Maximum Bipartite Matching
Channel Assignment Problem
Introduction to Push Relabel Algorithm
Introduction and implementation of Karger's algorithm for Minimum Cut
Dinic's algorithm for Maximum Flow

Some must do problems on Graph

Find size of the largest region in Boolean Matrix
Count number of trees in a forest
A Peterson Graph Problem
Clone an Undirected Graph
Introduction to Graph Coloring

Traveling Salesman Problem (TSP) Implementation

Introduction and Approximate Solution for Vertex Cover Problem
Erdos Renyl Model (for generating Random Graphs)
Chinese Postman or Route Inspection | Set 1 (introduction)
Hierholzer's Algorithm for directed graph
Boggle (Find all possible words in a board of characters) | Set 1
Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
Construct a graph from given degrees of all vertices
Determine whether a universal sink exists in a directed graph
Number of sink nodes in a graph
Two Clique Problem (Check if Graph can be divided in two Cliques)

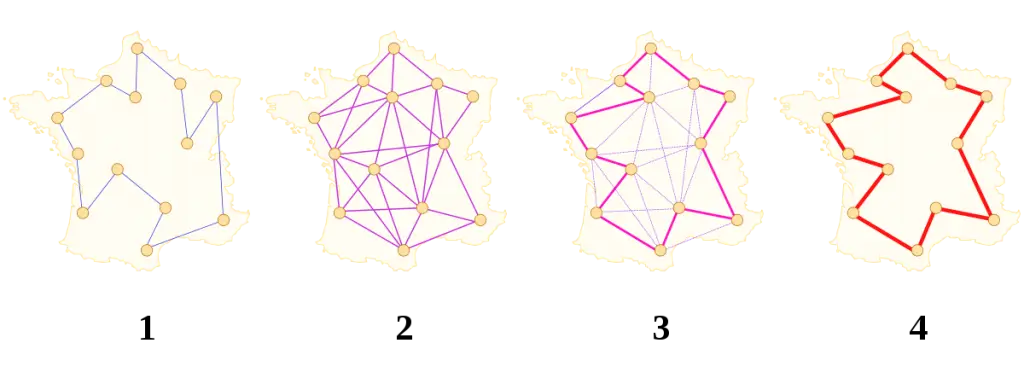
Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle. For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.

Examples:

In this post, the implementation of a simple solution is discussed.

Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
Generate all (n-1)! permutations of cities.
Calculate the cost of every permutation and keep track of the minimum cost permutation.
Return the permutation with minimum cost.

Below is the implementation of the above idea

Time complexity: O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set. Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Forgot password? New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with $n$ cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are $4!$, or 24, paths. However, if the size of this map is increased to 20 cities, there will be $1.22 \cdot 10^{17}$ paths!

The greedy approach to TSP would go like this:

Find all possible paths.
Find the cost of every paths.
Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of $O(n!)$. However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at $O(n^2 2^n)$. Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a $3/2$ approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then $P = NP$. As it stands, most scientists believe that $P \ne NP$.

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

2.1 Graph Theory
2.2 Classifications of the TSP
2.3 Variations of the TSP
3.1 aTSP ILP Formulation
3.2 sTSP ILP Formulation
4.1 Exact algorithms
4.2.1 Tour construction procedures
4.2.2 Tour improvement procedures
5 Applications
7 References

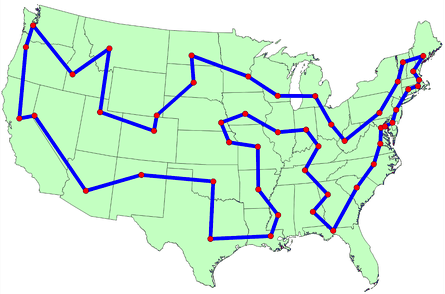
The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

$G=(V,E)$

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

$C$

Applies when the distance between cities is the same in both directions

$\exists ~i,j:c_{ij}\neq c_{ji}$

Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

$u$

Formulation

$n$

The objective function is then given by

${\text{min}}\sum _{i}\sum _{j}c_{ij}y_{ij}$

To ensure that the result is a valid tour, several contraints must be added. 1,3

$\sum _{j}y_{ij}=1,~~\forall i=0,1,...,n-1$

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

${\begin{aligned}{\text{min}}&~~\sum _{i}\sum _{j}c_{ij}y_{ij}\\{\text{s.t}}&~~\sum _{j}y_{ij}=1,~~i=0,1,...,n-1\\&~~\sum _{i}y_{ij}=1,~~j=0,1,...,n-1\\&~~\sum _{i}\sum _{j}y_{ij}\leq |S|-1~~S\subset V,2\leq |S|\leq n-2\\&~~y_{ij}\in \{0,1\},~\forall i,j\in E\\\end{aligned}}$

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

${\begin{aligned}{\text{min}}&~~\sum _{i}\sum _{j}c_{ij}y_{ij}\\{\text{s.t}}&~~\sum _{i<k}y_{ik}+\sum _{j>k}y_{kj}=2,~~k\in V\\&~~\sum _{i}\sum _{j}y_{ij}\leq |S|-1~~S\subset V,3\leq |S|\leq n-3\\&~~y_{ij}\in \{0,1\}~\forall i,j\in E\\\end{aligned}}$

Exact algorithms

$O(n!)$

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

Tour construction procedures where a solution is gradually built by adding a new vertex at each step
Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

$k$

Tour improvement procedures

$t$

Applications

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

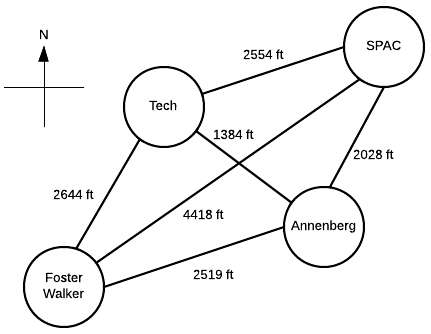
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

Drop off a homework set at Tech
Work out a SPAC
Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

Smallest distance is from Foster-Walker is to Annenberg
Smallest distance from Annenberg is to Tech
Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
Next smallest distance from Tech is to SPAC
Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

Smallest distance is Annenberg → Tech
Next smallest is SPAC → Annenberg
Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
Next smallest is Tech → Foster-Walker
Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

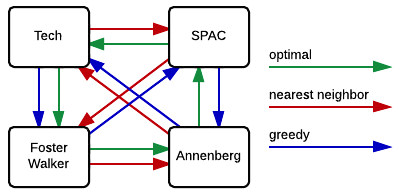
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
Goyal, S. (n.d.). A suvey on travlling salesman problem.

What is the Travelling Salesperson Problem (TSP)?

Breaking down the Travelling Salesperson Problem (TSP), a classic optimization issue in computer science that involves finding the shortest possible route through a set of locations.

Your all-in-one local delivery app for Shopify

The Travelling Salesperson Problem (TSP), or sometimes known as the Travelling Salesman Problem, is the challenge of determining the quickest path for your delivery drivers, field sales representatives, and service reps given a list of specific locations.

Let’s look at an example to better grasp the issue: A salesman wants to sell his products in a few different places. He is familiar with the names of the locations as well as the distances between them.

What is the quickest route for the salesman to take to visit each place only once before returning to the starting point?

The problem you just read is the well-known problem of the travelling salesperson.

The TSP is an old problem in computer science that has ramifications in complexity theory and the P versus NP dilemma. It is an extension of the Hamiltonian Circuit Problem .

The Travelling Salesperson Problem and the Vehicle Routing Problem (VRP) are also generalizations of TSP.

Below, we go over the Travelling Salesperson Problem in great depth.

About the travelling salesperson problem, why is it so difficult to solve the travelling salesperson problem, applications for the travelling salesperson problem, challenges faced by travelling salespeople, how to solve the travelling salesperson problem by using a route planner, final thoughts on the travelling salesperson problem.

Even though the travelling salesman problem (TSP) was first proposed in 1930, it remains one of the most researched combinatorial optimization problems today.

Richard Karp established in 1972 that the Hamiltonian cycle problem, a class of combinatorial optimization problems, was NP-complete.

This suggests that the TSP was NP-hard , and that determining the optimum route becomes exponentially more difficult as additional destinations are added to the issue.

For example, if there are four cities, there are three possible routes; but, if there are six cities, there are 360 possible ways.

This is due to the fact that scientists compute not only the most efficient approach, but also the one that works.

This algorithm employs the brute-force method, which entails calculating every possible solution and then selecting the best one. To put it another way, look for every possible twist and turn the salesman might take.

Since the early 1990s , computer scientists have been able to determine the ideal solution to this problem for thousands of cities, despite the fact that computing challenges rise with each additional city added to the itinerary.

Many towns and cities in a US state, for example, could be included in the delivery region of a large logistics provider.

It would save a lot of time and money to figure out the shortest route between all of the stops the vehicle needs to make on a daily basis.

The TSP is simple to state in theory, and it can be solved by checking all round-trip routes to identify the shortest one.

However, when the number of cities increases, the number of round-trips required exceeds the capabilities of even the most powerful computers.

With ten cities, more than 300,000 round-trip permutations and combinations are possible.

With 15 cities, there might be more than 87 billion different paths.

Computer scientists hoped that someone would come up with a better algorithm or strategy for solving the travelling salesman issue in a reasonable amount of time in the early days of computers.

While scientists progressed with specific cases, there was no effective travelling salesman problem solver accessible.

It’s likely that a one-size-fits-all algorithm isn’t even possible.

The TSP is still used in a variety of industries. The TSP’s efficient solutions have been used to astronomy, computer science, and even vehicle navigation.

The travelling salesperson problem can also be used to determine how a laser should move when boring points into a PCB.

TSP ideas are used by astronomers to calculate the movement of a telescope for the shortest distance between stars in a constellation.

TSP can also be used for internet planning, agribusiness, microchip manufacturing, and computer-generated art.

Almost every salesman thinks about how to make the most of their day when they get up.

They have a lot of scheduled appointments with their consumers, as well as a lot of last-minute ones.

Salespeople’s schedules aren’t usually set in stone. Salespeople are frequently forced to retrace and take longer routes to reach customer locations as a result of this flaw.

Missed appointments and opportunities come from this lack of route planning .

In addition to the route issues that plagued yesteryear’s salesperson, today’s salesperson encounters traffic congestion, last-minute customer requests, and strict delivery window timings.

Try this: If you thought the TSP from the mathematics puzzle was challenging, consider these questions:

What if you had to plan routes for more than one salesperson?
What if you had a sales staff on your side?
What if you had to divide and conquer the visits with your team?
What if salespeople had varied appointment slots and your goal was to maintain their routes as short, quick, and efficient as possible?

Think about the following scenario: If your company has 100 customer addresses and eight salesmen, there could be over a million possible route permutations.

It will take days, if not months, to run a rudimentary algorithm that weighs every conceivable combination and selects the best one.

That’s a real-world problem, and that’s where route optimization comes in.

The goal of a route optimizer is to determine the quickest, shortest, and most fuel-efficient route between two points.

Route planning will inevitably become too complex to manage with pen and paper or common technologies like Google Maps or Waze as your delivery business grows. If route planning is done manually, sticking to schedules may be difficult, if not impossible.

Without route planning software, you won’t be able to manually factor in variables like customer time windows and weather conditions, and you’ll end up spending a lot of time arranging routes.

Unexpected circumstances, such as road congestion or construction, might make keeping your field reps on schedule and meeting consumers on time difficult. You also risk boosting your operating costs, which would most likely come in the form of wasted gasoline and salaries as a result of the lengthier driving time.

Furthermore, if your salespeople are late for meetings or your delivery drivers are late, your clients will have a negative first impression.

In a matter of minutes, a trustworthy route optimization program like EasyRoutes will help you decrease driving time and fuel consumption by determining the most effective route for your team.

It’s a tool that effectively addresses the difficult Travelling Salesperson Problem of determining the most efficient path to a location. The Travelling Salesperson Problem has no human answer; finding the most efficient path is physically impossible, but it is conceivable to find a highly efficient route or one that is more efficient than humans could ever be by using advanced routing software.

A route planner will assist in ensuring on-time customer encounters, cost savings, and the safety of field workers. This is because we all have a tendency to drive quickly in order to “make up” for lost time, which increases the danger of an accident.

A route optimizer will also cut down on your field service personnel’ driving time, allowing them to spend more time with clients and improving your bottom line.

If you look around, there will be many more TSP-like situations with people and vehicles dealing with erroneous routes and delays.

The couriers who are delivering packages to your place of business.
The delivery team is sending you fresh groceries the same day you placed your purchase.
The school buses that always arrive on schedule and pick up and drop off your children at the same time each day.

For decades, scientists have been attempting to solve challenges like TSP. Complex algorithms via easy-to-use route planner apps are the closest we’ve come.

About Roundtrip

Roundtrip's mission is to equip every business with the software tools they need to deliver products to their customers in a delightful way. Thousands of Shopify merchants worldwide choose EasyRoutes to power their local deliveries across dozens of product categories, from meal kits and groceries to coffee, cupcakes, kibble, and so much more. Our easy-to-use route planning and delivery optimization app is certified Built for Shopify, a two-time Shopify staff pick, and the top rated local delivery app on the Shopify App Store.

Check out these other articles

Use Delivery Management Software to Deliver Profits

How to Select the Right Route Planner for Your Deliveries

Drive Success: Optimize Routes, Reduce Costs

Designed to make deliveries easy

EasyRoutes gives you full control over your delivery workflow — all from within your Shopify admin.

Explained: What is Traveling Salesman Problem (TSP)

Last Updated: January 24, 2023

A well-known mathematical problem called the Traveling Salesman Problem (TSP) aims to determine the shortest path between a number of places.
Logistics, transportation, and manufacturing are just a few of the industries where the TSP is useful.
The number of points, the form of the point set, and the algorithm employed can all have an impact on how the TSP is solved.
Technology advancements like cloud computing and parallel processing have made it possible to solve the Traveling Salesman Problem effectively for larger and more complicated situations.

Traveling salesman problem is not new for delivery-based businesses. Its recent expansion has insisted that industry experts find optimal solutions in order to facilitate delivery operations.

The major challenge is to find the most efficient routes for performing multi-stop deliveries. Without the shortest routes, your delivery agent will take more time to reach the final destination. Sometimes problems may arise if you have multiple route options but fail to recognize the efficient one.

Eventually, traveling salesman problem would cost you time and result in late deliveries . So, before it becomes an irreparable issue for your delivery company, let us understand the traveling salesman problem and find optimal solutions in this blog.

Table of Content

What is the Traveling Salesman Problem (TSP)?
Commom challenges of Traveling Salesman Problem (TSP)

What are Some Popular Solutions to Traveling Salesman Problem?

What are other optimal solutions to the traveling salesman problem, what are some real-life applications of traveling salesman problem.

How TSP and VRP Combinedly Pile up Challenges?
Can a route planner resolve Traveling Salesman Problem (TSP)?

What is Traveling Salesman Problem (TSP)?

The traveling Salesman Problem (TSP) is a combinatorial problem that deals with finding the shortest and most efficient route to follow for reaching a list of specific destinations.

It is a common algorithmic problem in the field of delivery operations that might hamper the multiple delivery process and result in financial loss. TSP turns out when you have multiple routes available but choosing a minimum cost path is really hard for you or a traveling person.

How difficult is it to solve?

It is quite difficult to solve TSP as it is known as NP-hard, which means there is no polynomial time algorithm to solve it for more numbers of addresses. So, with an increasing amount of addresses, the complexity of solving TSP increases exponentially.

So, it is impossible to find TSP solutions manually. Also, many mathematical algorithms and the fastest computers fail to solve TSP.

However, TSP can be eliminated by determining the optimized and efficient path using approximation algorithms or automated processes.

Common Challenges of Traveling Salesman Problem (TSP)

Being a salesman is not easy, as you need to face various unavoidable challenges in your everyday schedules.

Firstly, every day, salespeople have to carry out a number of deliveries in a very limited time, so there are a lot of time constraints. To overcome this, you need to plan your routes in a way that you make the most out of them.
Secondly, there are chances of last-minute changes. Sometimes you get extra and urgent visits to make, while sometimes, some visits are postponed or canceled due to the customer’s unavailability.
Lastly, a math problem, a combinatorial optimization problem, arises. A combinatorial optimization problem is a problem that is mathematically complex to solve as you have to deal with many variables.

These are major challenges in the Traveling Salesman Problem (TSP) as you are required to create a route with the shortest distances using hundreds and thousands of permutations and combinations that asks for less fuel, fulfill on-time delivery to customers, and are ready to modify routes considering last minute changes.

These are some of the near-optimal solutions to find the shortest route to a combinatorial optimization problem.

1. Nearest Neighbor (NN)

The Nearest Neighbor Method is probably the most basic TSP heuristic. The method followed by this algorithm states that the driver must start by visiting the nearest destination or closest city. Once all the cities in the loop are covered, the driver can head back to the starting point.

Solving TSP using this efficient method, requires the user to choose a city at random and then move on to the closest unvisited city and so on. Once all the cities on the map are covered, you must return to the city you started from.

2. The Branch and Bound Algorithm

The Branch and Bound Algorithm for traveling salesman problem

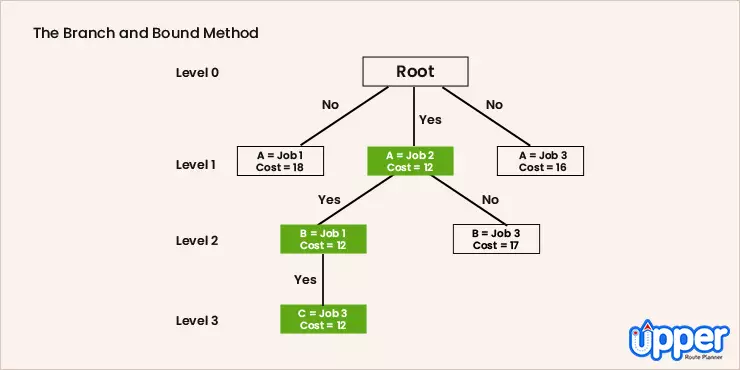
The Branch & Bound method follows the technique of breaking one problem into several little chunks of problems. So it solves a series of problems. Each of these sub-problems may have multiple solutions. The solution you choose for one problem may have an effect on the solutions of subsequent sub-problems.

3. The Brute Force Algorithm

Brute Force Algorithm to solve traveling salesman problem

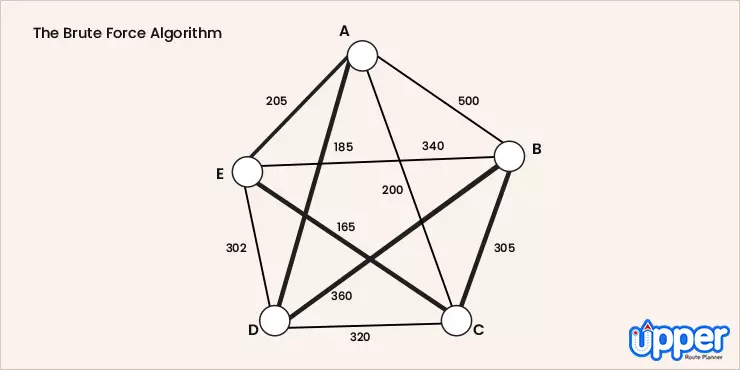
The Brute Force Approach takes into consideration all possible minimum cost permutation of routes using a dynamic programming approach. First, calculate the total number of routes. Draw and list all the possible routes that you get from the calculation. The distance of each route must be calculated and the shortest route will be the most optimal solution.

Other Optimal Solutions to the Traveling Salesman Problem

Multi-Agent System : Involves distributing the pair of cities into groups. Then assign a single agent to discover the shortest path, covering all the cities in the assigned group.
Zero Suffix Method : This method solves the classical symmetric TSP and was introduced by Indian researchers.
Multi-Objective Evolutionary Algorithm : This method solves the TSP using NSGA-II
Biogeography-based Optimization Algorithm : This method is based on the migration strategy of animals for solving optimization issues.
Meta-Heuristic Multi Restart Iterated Local Search : This method states that the technique is more efficient compared to genetic algorithms.

Blow Away TSP using Upper

Need a permanent solution for recurring TSP? Sign up with Upper to keep your tradesmen updated all the time. Lay off your manual calculation and adopt an automated process now!

Most businesses see a rise in the Traveling Salesman Problem (TSP) due to the last mile delivery challenges . The last mile delivery is the process of delivering goods from the warehouse (or a depot) to the customer’s preferred location. Considering the supply chain management, it is the last mile deliveries that cost you a wholesome amount.

At the same time, you need to sacrifice financial loss in order to maintain your current position in the market. Suppose last mile delivery costs you $11, the customer will pay $8 and you would suffer a loss. This is because of pre-defined norms which may favor the customer to pay less amount.

Real-Life Applications of Traveling Salesman Problem

This hefty last mile delivery cost is the result of a lack of Vehicle routing problem(VRP) software. VRP finds you the most efficient routes so that operational costs will not get increase. So, by using the right VRP software, you would not have to bother about TSP.

Such delivery management software uses an automated process that doesn’t need manual intervention or calculations to pick the best routes. Hence, it is the easiest way to get rid of the traveling Salesman Problem (TSP).

How TSP and VRP Combinedly Pile Up Challenges?

The traveling Salesman Problem is an optimization problem studied in graph theory and the field of operations research. In this optimization problem, the nodes or cities on the graph are all connected using direct edges or routes. The weight of each edge indicates the distance covered on the route between the two cities.

The problem is about finding an optimal route that visits each city once and returns to the starting and ending point after covering all cities once.

The TSP is often studied in a generalized version which is the Vehicle Routing Problem . It is one of the most broadly worked on problems in mathematical optimization. VRP deals with finding or creating a set of routes for reducing time, fuel, and delivery costs.

Is there any real world solution to TSP and VRP?

Many solutions for TSP and VRP are based on academics which means they are not so practical in everyday life. The reason is that many of them are just limited to perfection, but need a dynamic programming-based solution. So, if businesses really want to get rid of them, they need a TSP solver integrated with route optimization software.

The right TSP solver will help you disperse such modern challenges. It offers in-built route planning and optimization solutions in such a way that your tradesman doesn’t get stranded while delivering the parcel. Also, it is equipped with an efficient algorithm that provides true solutions to the TSP. As a result, the delivery manager can create a route plan hassle-free in a few minutes.

Can a Route Planner Resolve the Traveling Salesman Problem (TSP)?

In the general case, the Traveling Salesman Problem (TSP) involves finding the shortest optimized and possible route that includes a set of stops and returns to the starting point. The number of possible routes increases exponentially as the number of locations increases. Finding the best solution becomes difficult computationally, even for moderately sized problems.

But, Upper Route Planner, a route optimization software , is built differently. Upper has all the solutions you need when talking about TSP.

For example, if you are in charge of planning delivery routes with more than 500 stops in them, all you need to do is import an Excel or CSV file with multiple addresses into Upper, review, allot delivery drivers, optimize, and dispatch with a single click. This delivery route planning solution saves you hours of time spent on planning delivery routes and optimizing them.

Also, once the delivery is completed, Upper lets you collect proof of delivery. This is how the Upper Route Planner is a simple solution to the Traveling Salesman Problem.

Upper Route Planner

A simple-to-use route planner that every one is talking about

TSP stands for traveling Salesman Problem, while VRP is an abbreviation form of vehicle routing problem (VRP). In the delivery industry, both of them are widely known by their abbreviation form.

Yes, you can prevent TSP by using the right route planner. The online route planner helps you get the optimized path so that your delivery agents don’t have to deal with such challenges. In addition, they don’t struggle with multiple routes. Instead, they can progress on the shortest route.

The new method has made it possible to find solutions that are almost as good. This was done by the Christofides algorithm, the popular algorithm in theoretical computer science. This algorithm plugs into an alternate version of the problem that finds a combination of paths as per permutations of cities. It made the round trip route much longer. The round trip produced by the new method, while still not being efficient enough is better than the old one.

The vehicle routing problem (VRP) reduces the transportation costs as well as drivers’ expenses. It helps you serve more customers with fewer fleets and drivers. Thus, you don’t have any variation in the time taken to travel.

Create Optimized Routes Using Upper and Bid Goodbye to Traveling Salesman Problem

As a business owner, If you are dealing with TSP and want to get rid of them, we recommend using a TSP solver like Upper Route Planner. The online route planner is capable of plucking out the most efficient routes no matter how big your TSP is. It has an in-built sophisticated algorithm that helps you get the optimized path in a matter of seconds.

Therefore, you won’t fall prey to such real-world problems and perform deliveries in minimum time. Upper’s delivery route planner offers a dedicated driver app that makes sure your tradesman doesn’t go wrongfooted and quickly wraps up pending deliveries. Don’t just agree with our words, book a demo on Upper and disperse TSP once and for all.

Rakesh Patel, author of two defining books on reverse geotagging, is a trusted authority in routing and logistics. His innovative solutions at Upper Route Planner have simplified logistics for businesses across the board. A thought leader in the field, Rakesh's insights are shaping the future of modern-day logistics, making him your go-to expert for all things route optimization. Read more.

Get weekly updates from Upper Route Planner.

Tired of Manual Routing?

Sales route planning: How to find the best sales routes

Sales Route Planning Guide: Know How to Plan the Best Sales Routes

https://www.upperinc.com/guides/travelling-salesman-problem/

Grab a FREE Trial of Upper

Plan routes with hundreds of stops in a minute
Schedule routes months in advance
Collect reliable proof of delivery
Track drivers live for real-time updates
Experience unparalleled customer support

Grab a FREE Trial of Upper TODAY!

Schedule routes in advance for weeks
Collect proof of delivery to maintain accountability
Experience 24/7 customer support
Smart reporting to get real-time insights

12.9 Traveling Salesperson Problem

Learning objectives.

After completing this section, you should be able to:

Distinguish between brute force algorithms and greedy algorithms.
List all distinct Hamilton cycles of a complete graph.
Apply brute force method to solve traveling salesperson applications.
Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths . In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

Design of fiber optic networks
Minimizing fuel expenses for repositioning satellites
Development of semi-conductors for microchips
A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

An algorithm is a sequence of steps that can be used to solve a particular problem. We have solved many problems in this chapter, and the procedures that we used were different types of algorithms. In this section, we will use two common types of algorithms, a brute force algorithm and a greedy algorithm . A brute force algorithm begins by listing every possible solution and applying each one until the best solution is found. A greedy algorithm approaches a problem in stages, making the apparent best choice at each stage, then linking the choices together into an overall solution which may or may not be the best solution.

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.187 . Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

After phase 2, based on the information you have, you will choose the branch with 10, 7 and 4. Now, you are following a different branch than before, but it is the best choice based on the information you have. Let’s look at the last phase.

After phase 3, you will choose branch G which has a sum of 32.

The process of adding the values on each branch and selecting the highest sum is an example of a brute force algorithm because all options were explored in detail. The process of choosing the branch in phases, based on the best choice at each phase is a greedy algorithm. Although a brute force algorithm gives us the ideal solution, it can take a very long time to implement. Imagine a tree diagram with thousands or even millions of branches. It might not be possible to check all the sums. A greedy algorithm, on the other hand, can be completed in a relatively short time, and generally leads to good solutions, but not necessarily the ideal solution.

Example 12.42

Distinguishing between brute force and greedy algorithms.

A cashier rings up a sale for $4.63 cents in U.S. currency. The customer pays with a $5 bill. The cashier would like to give the customer $0.37 in change using the fewest coins possible. The coins that can be used are quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). The cashier starts by selecting the coin of highest value less than or equal to $0.37, which is a quarter. This leaves $ 0.37 − $ 0.25 = $ 0.12 $ 0.37 − $ 0.25 = $ 0.12 . The cashier selects the coin of highest value less than or equal to $0.12, which is a dime. This leaves $ 0.12 − $ 0.10 = $ 0.02 $ 0.12 − $ 0.10 = $ 0.02 . The cashier selects the coin of highest value less than or equal to $0.02, which is a penny. This leaves $ 0.02 − $ 0.01 = $ 0.01 $ 0.02 − $ 0.01 = $ 0.01 . The cashier selects the coin of highest value less than or equal to $0.01, which is a penny. This leaves no remainder. The cashier used one quarter, one dime, and two pennies, which is four coins. Use this information to answer the following questions.

Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Now let’s focus our attention on the graph theory application known as the traveling salesperson problem (TSP) in which we must find the shortest route to visit a number of locations and return to the starting point.

Recall from Hamilton Cycles , the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.192 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

Any route that visits each base and returns to the start would be a Hamilton cycle on the graph. If the officer wants to travel the shortest distance, this will correspond to a Hamilton cycle of lowest weight. We saw in Table 12.11 that there are six distinct Hamilton cycles (directed cycles) in a complete graph with four vertices, but some lie on the same cycle (undirected cycle) in the graph.

Since the distance between bases is the same in either direction, it does not matter if the officer travels clockwise or counterclockwise. So, there are really only three possible distances as shown in Figure 12.193 .

The possible distances are:

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

Notice that we listed all of the Hamilton cycles and found their weights when we solved the TSP about the officer from Vandenberg. This is a skill you will need to practice. To make sure you don't miss any, you can calculate the number of possible Hamilton cycles in a complete graph. It is also helpful to know that half of the directed cycles in a complete graph are the same cycle in reverse direction, so, you only have to calculate half the number of possible weights, and the rest are duplicates.

In a complete graph with n n vertices,

The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

TIP! When listing all the distinct Hamilton cycles in a complete graph, you can start them all at any vertex you choose. Remember, the cycle a → b → c → a is the same cycle as b → c → a → b so there is no need to list both.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
Which pairs of cycles must have the same weights? How do you know?
There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
Yes, they are all distinct cycles and there are 6 of them.
Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

TIP! When listing the possible cycles, ignore the vertex where the cycle begins and ends and focus on the ways to arrange the letters that represent the vertices in the middle. Using a systematic approach is best; for example, if you must arrange the letters M, O, and P, first list all those arrangements beginning with M, then beginning with O, and then beginning with P, as we did in Example 12.42.

Your Turn 12.43

The brute force method.

The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method . The steps in the brute force method are:

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

On the next assignment, the air force officer must leave from Travis Air Force base, visit Beal, Edwards, and Vandenberg Air Force bases each exactly once and return to Travis Air Force base. There is no need to visit Los Angeles Air Force base. Use Figure 12.194 to find the shortest route.

Step 1: Since there are 4 vertices, there will be ( 4 − 1 ) ! = 3 ! = 6 ( 4 − 1 ) ! = 3 ! = 6 cycles, but half of them will be the reverse of the others; so, there will be ( 4 − 1 ) ! 2 = 6 2 = 3 ( 4 − 1 ) ! 2 = 6 2 = 3 possible distances.

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.195 .

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

The second path, T → B → V → E → T , and its reverse, T → E → V → B → T , have the least weight. The solution is that the officer should travel from Travis Air Force base to Beal Air Force Base, to Vandenberg Air Force base, to Edwards Air Force base, and return to Travis Air Force base, or the same route in reverse.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.194 . There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

When the brute force method is impractical for solving a traveling salesperson problem, an alternative is a greedy algorithm known as the nearest neighbor method , which always visit the closest or least costly place first. This method finds a Hamilton cycle of relatively low weight in a complete graph in which, at each phase, the next vertex is chosen by comparing the edges between the current vertex and the remaining vertices to find the lowest weight. Since the nearest neighbor method is a greedy algorithm, it usually doesn’t give the best solution, but it usually gives a solution that is "good enough." Most importantly, the number of steps will be the number of vertices. That’s right! A problem with 10 vertices requires 10 steps, not 362,880. Let’s look at an example to see how it works.

Suppose that a candidate for governor wants to hold rallies around the state. They plan to leave their home in city A , visit cities B, C, D, E , and F each once, and return home. The airfare between cities is indicated in the graph in Figure 12.196 .

Let’s help the candidate keep costs of travel down by applying the nearest neighbor method to find a Hamilton cycle that has a reasonably low weight. Begin by marking starting vertex as V 1 V 1 for "visited 1st." Then to compare the weights of the edges between A and vertices adjacent to A : $250, $210, $300, $200, and $100 as shown in Figure 12.197 . The lowest of these is $100, which is the edge between A and F .

Mark F as V 2 V 2 for "visited 2nd" then compare the weights of the edges between F and the remaining vertices adjacent to F : $170, $330, $150 and $350 as shown in Figure 12.198 . The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 V 3 for "visited 3rd." Next, compare the weights of the edges between D and the remaining vertices adjacent to D : $120, $310, and $270 as shown in Figure 12.199 . The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 V 4 for "visited 4th." Finally, compare the weights of the edges between B and the remaining vertices adjacent to B : $160 and $220 as shown in Figure 12.200 . The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 V 5 and mark the only remaining vertex, which is C , as V 6 V 6 . This is shown in Figure 12.201 . Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

The Hamilton cycle we found is A → F → D → B → E → C → A . The weight of the circuit is $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 . This may or may not be the route with the lowest cost, but there is a good chance it is very close since the weights are most of the lowest weights on the graph and we found it in six steps instead of finding 120 different Hamilton cycles and calculating 60 weights. Let’s summarize the procedure that we used.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 2: Label the vertex at the end of the edge of lowest weight that you found in previous step as V n V n where the subscript n indicates the order the vertex is visited. Identify the edge of lowest weight between V n V n and the vertices that remain to be visited.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.202 . Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Step 3: A Hamilton cycle of low weight is A → D → F → C → B → E → A . So, a route of relatively low travel time is A to D to F to C to B to E and back to A . The total travel time of this route is: 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min

Your Turn 12.45

Check your understanding, section 12.9 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

Authors: Donna Kirk
Publisher/website: OpenStax
Book title: Contemporary Mathematics
Publication date: Mar 22, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
Section URL: https://openstax.org/books/contemporary-mathematics/pages/12-9-traveling-salesperson-problem

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

12.10: Traveling Salesperson Problem

Last updated
Save as PDF
Page ID 129677

Learning Objectives

After completing this section, you should be able to:

Distinguish between brute force algorithms and greedy algorithms.
List all distinct Hamilton cycles of a complete graph.
Apply brute force method to solve traveling salesperson applications.
Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths. In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

Design of fiber optic networks
Minimizing fuel expenses for repositioning satellites
Development of semi-conductors for microchips
A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.214. Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

$A graph has 15 vertices. The vertices are labeled 1 to 15. 10 branches into 2 and 7. 2 branches into 11 and 15. 11 branches into 13 and 8. 15 branches into 1 and 6. 7 branches into 3 and 4. 3 branches into 20 and 14. 4 branches into 11 and 5. 13, 8, 1, 6, 20, 14, 11, and 5 are labeled A to H.$

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

$A graph has 3 vertices. The vertices are labeled 10, 2, and 7. 10 branches into 2 and 7. The edge, 10 to 7 is highlighted.$

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

$A graph has 5 vertices. The vertices are labeled 10, 2, 7, 3, and 4. 10 branches into 2 and 7. 7 branches into 3 and 4. The edges, 10 to 7 and 7 to 4 are highlighted.$

$A graph has 7 vertices. The vertices are labeled 10, 2, 7, 3, 4, 11, and 15. 10 branches into 2 and 7. 7 branches into 3 and 4. 4 branches into 11 and 5. The edges, 10 to 7, 7 to 4, and 4 to 11 are highlighted. 11 and 5 are labeled G and H.$

After phase 3, you will choose branch G which has a sum of 32.

Example 12.42

Distinguishing between brute force and greedy algorithms.

Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Recall from Hamilton Cycles, the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.219 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

$A graph represents the four California air force bases. The graph has four vertices: E, B, V, and L. The edge, E B is labeld 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles.$

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines.$

a → b → c → d → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, ad, and bc are in dashed lines. Directed edges flow from a to b, b to d, d to c, and c to a.$

a → b → d → c → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and dc are in dashed lines. Directed edges flow from a to c, c to b, b to d, and d to a.$

a → c → b → d → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines. Directed edges flow from a to d, d to c, c to b, and b to a.$

a → d → c → b → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a d, and bc are in dashed lines. The directed edges flow from a to c, c to d, d to b, and b to a.$

a → c → d → b → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and dc are in dashed lines. The edges flow from a to d, d to b, b to c, and c to a.$

a → d → b → c → a

$Three graphs represent the four California air force bases. Each graph has four vertices: E, B, V, and L. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. In the first graph, the edges, E V, and L B are in dashed lines. In the second graph, the edges, E L and B V are in dashed lines. In the third graph, the edges, E B and L V are in dashed lines.$

The possible distances are:

396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148 396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

In a complete graph with n n vertices,

The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
Which pairs of cycles must have the same weights? How do you know?
There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
Yes, they are all distinct cycles and there are 6 of them.
Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

Your Turn 12.43

The brute force method.

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

$A graph represents the five California air force bases. The graph has five vertices: E, B, V, L, and T. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. The edge, E T is labeled 370 miles. The edge, L T is labeled 396 miles. The edge, B T is labeled 84 miles. The edge, V T is labeled 396 miles.$

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.222.

$A graph represents four cities. The graph has five vertices: E, B, V, L, and T. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. The edge, E T is labeled 370 miles. The edge, L T is labeled 396 miles. The edge, B T is labeled 84 miles. The edge, V T is labeled 396 miles. The edges, E L, L V, L B, and L T are in dashed lines.$

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.221. There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

$A graph represents the airfares between six different cities. The graph has 6 vertices. The vertices are A, B, C, D, E, and F. Edges from A leading to B, C, D, E, and F are labeled 250 dollars, 210 dollars, 300 dollars, 200 dollars, and 100 dollars. Edges from B leading to C, D, E, and F are labeled 220 dollars, 120 dollars, 160 dollars, and 170 dollars. Edges from C to D, E, and F are labeled 310 dollars, 180 dollars, and 330 dollars. Edges from D to E and F 270 dollars and 150 dollars. An edge from E to F is labeled 350 dollars.$

Mark F as V 2 Figure 12.225. The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 Figure 12.226. The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 Figure 12.227. The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 Figure 12.228. Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.229. Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

$A graph represents the airfares between six different cities. The graph has 6 vertices. The vertices are A, B, C, D, E, and F. Edges from A leading to B, C, D, E, and F are labeled 120 minutes, 140 minutes, 85 minutes, 90 minutes, and 180 minutes. Edges from B leading to C, D, E, and F are labeled 100 minutes, 80 minutes, 95 minutes, and 110 minutes. Edges from C to D, E, and F are labeled 220 minutes, 200 minutes, and 75 minutes. Edges from D to E and F are labeled 130 minutes and 70 minutes. An edge from E to F is labeled 210 minutes.$

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Your Turn 12.45

Check your understanding, section 12.9 exercises.

$Four graphs. Graph A has four vertices: a, b, c, and d. The edges are labeled as follows: a b, 3; b d, 3; d c, 1; c a, 2; a d, 1; b c, 2. Graph B has five vertices: e, f, g, h, and I. The edges are labeled as follows: e f, 2-thirds; f g, 5-twelfths; g h, 1-twelfth; h i, 3-fourths; i e, 1-fourth; e h, 1-half; e g, 1-sixth; f i, -third; f h, 5-sixths; g i, 1. Graph C has five vertices: i, j, k, m, and n. The curved edges are labeled as follows: k m, 20; m n, 30; n j, 40; j i, 50; i k, 10. The straight edges are labeled as follows: k j, 90; k n, 60; m i, 100; m j, 70; n i, 80. Graph d has four vertices; o, p, q, and r. The edges are labeled as follows: o p, 1.7; p q, 4.3; q r, 3.5; r o, 2.9 p r, 3.; o p, 1.2.$

Data Structures & Algorithms
DSA - Overview
DSA - Environment Setup
DSA - Algorithms Basics
DSA - Asymptotic Analysis
Data Structures
DSA - Data Structure Basics
DSA - Data Structures and Types
DSA - Array Data Structure
Linked Lists
DSA - Linked List Data Structure
DSA - Doubly Linked List Data Structure
DSA - Circular Linked List Data Structure
Stack & Queue
DSA - Stack Data Structure
DSA - Expression Parsing
DSA - Queue Data Structure
Searching Algorithms
DSA - Searching Algorithms
DSA - Linear Search Algorithm
DSA - Binary Search Algorithm
DSA - Interpolation Search
DSA - Jump Search Algorithm
DSA - Exponential Search
DSA - Fibonacci Search
DSA - Sublist Search
DSA - Hash Table
Sorting Algorithms
DSA - Sorting Algorithms
DSA - Bubble Sort Algorithm
DSA - Insertion Sort Algorithm
DSA - Selection Sort Algorithm
DSA - Merge Sort Algorithm
DSA - Shell Sort Algorithm
DSA - Heap Sort
DSA - Bucket Sort Algorithm
DSA - Counting Sort Algorithm
DSA - Radix Sort Algorithm
DSA - Quick Sort Algorithm
Graph Data Structure
DSA - Graph Data Structure
DSA - Depth First Traversal
DSA - Breadth First Traversal
DSA - Spanning Tree
Tree Data Structure
DSA - Tree Data Structure
DSA - Tree Traversal
DSA - Binary Search Tree
DSA - AVL Tree
DSA - Red Black Trees
DSA - B Trees
DSA - B+ Trees
DSA - Splay Trees
DSA - Tries
DSA - Heap Data Structure
DSA - Recursion Algorithms
DSA - Tower of Hanoi Using Recursion
DSA - Fibonacci Series Using Recursion
Divide and Conquer
DSA - Divide and Conquer
DSA - Max-Min Problem
DSA - Strassen's Matrix Multiplication
DSA - Karatsuba Algorithm
Greedy Algorithms
DSA - Greedy Algorithms
DSA - Travelling Salesman Problem (Greedy Approach)
DSA - Prim's Minimal Spanning Tree
DSA - Kruskal's Minimal Spanning Tree
DSA - Dijkstra's Shortest Path Algorithm
DSA - Map Colouring Algorithm
DSA - Fractional Knapsack Problem
DSA - Job Sequencing with Deadline
DSA - Optimal Merge Pattern Algorithm
Dynamic Programming
DSA - Dynamic Programming
DSA - Matrix Chain Multiplication
DSA - Floyd Warshall Algorithm
DSA - 0-1 Knapsack Problem
DSA - Longest Common Subsequence Algorithm
DSA - Travelling Salesman Problem (Dynamic Approach)
Approximation Algorithms
DSA - Approximation Algorithms
DSA - Vertex Cover Algorithm
DSA - Set Cover Problem
DSA - Travelling Salesman Problem (Approximation Approach)
Randomized Algorithms
DSA - Randomized Algorithms
DSA - Randomized Quick Sort Algorithm
DSA - Karger’s Minimum Cut Algorithm
DSA - Fisher-Yates Shuffle Algorithm
DSA Useful Resources
DSA - Questions and Answers
DSA - Quick Guide
DSA - Useful Resources
DSA - Discussion
Selected Reading
UPSC IAS Exams Notes
Developer's Best Practices
Questions and Answers
Effective Resume Writing
HR Interview Questions
Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

There’s only one edge between C → D, therefore it is added to the output graph.

There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

What is a Travelling Salesman Problem (TSP)? Explained!

Author: Diksha Bhandari
Read Time: 9 min
Published: September 14, 2023
Last Update: November 8th, 2023

Table of Contents

Asset Tracking
Dispatch Management
Driver Behaviour
Electric Vehicle
Employee Management
Field Sales And Service
Fleet Management
Fuel Management
GPS Software
GPS Trackers and Hardware
Last Mile Delivery
Lead Management
Leave And Attendance
Roster Management
Route Optimisation
Route Planning
Sensor Integration
Task and Workflow
Tech and Beyond
TrackoBit Industries
TrackoField
TrackoField Industries
TrackoMile Industries
Vehicle Tracking
Video telematics

What is a Traveling Salesman Problem (TSP)

Want to know what a travelling salesman problem (TSP) is? Need solutions to real-life TSP challenges. Learn here.

Do you also look for the shortest route on Google Maps before embarking on a trip?

I am sure, you know multiple routes to reach the office, the mall, or your desired location, but checking on the internet before leaving home has become a ritual. It becomes all the more important to refer to maps when you have to pick up friends or colleagues along the way.

‘ADD STOPS’

Yes, you are right! 💯

That’s what solving the TSP challenge using software means!

What is a Travelling Salesman Problem (TSP)?

The traveling salesman problem is the popular combinatorial optimisation challenge in mathematics and computer science. The prime objective of the problem is to determine the shortest possible route a salesperson must take to cover a set of locations in one go and then return to the starting point.

Addressing travelling salesman challenges and their optimisation are more relevant in this time and age, especially in the supply chain, logistics and delivery space.

TSP may result in delayed deliveries and slimming profits as it’s not easy for delivery agents to choose the most viable and cost-effective route in real-time.

What are Traveling Salesman Problem Challenges to Solve?

When a salesperson is in the field hopping from one client site to another, finding out the best and the shortest route is an added pressure on the agent. In today’s day and age, distance isn’t the only factor that defines efficiency. There are several factors, such as time, fuel consumption, capacity, etc. that together define efficiency.

However, addressing the travelling salesman challenges involves mitigating a few unavoidable challenges along the way that field agents face themselves.

1. Time Constraints

Sales agents often have a tight schedule with multiple deliveries to make with a short TAT. Similarly, in TSP, optimising routes to minimise travel time is a fundamental challenge.

2. Last-minute Changes

Eleventh-hour changes are not a new concept for salespeople. They encounter urgent visits and last-minute cancellations a lot. Similarly, TSP solutions must be adaptable to handle dynamic scenarios and route modifications.

3. Resource Efficiency

Just as salespersons aim at reducing fuel costs and ensuring on-time deliveries, TSP solutions such as TrackoMile must strive for resource optimisation by reducing travel distances and delivery TAT.

4. Objective Diversification

While solving the travelling salesman problem (TSP) , optimising multiple objectives such as cost, time, and environmental factors adds complexity as solutions need to balance conflicting goals.

5. Combinatorial Complexity

TSP is a combinatorial optimisation problem, which means it involves complicated mathematical calculations with numerous variables. Sometimes, complex scenarios get further intricate as multiple variables are involved.

6. Adaptability and Scalability

Similarly, how sales agents adjust to the routes on the fly, the route algorithm must be flexible and responsive to real-time changes such as spiking volumes, vehicle breakdown or traffic slow down. A TSP solution must have a good appetite to handle large datasets and complex networks.

Also Read 4 Key Solutions for Fuel Management System 2023

1. Brute Force Algorithm

The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all. While it guarantees an optimal solution, its downside lies in its major time complexity, making it practical only for small TSP challenges.

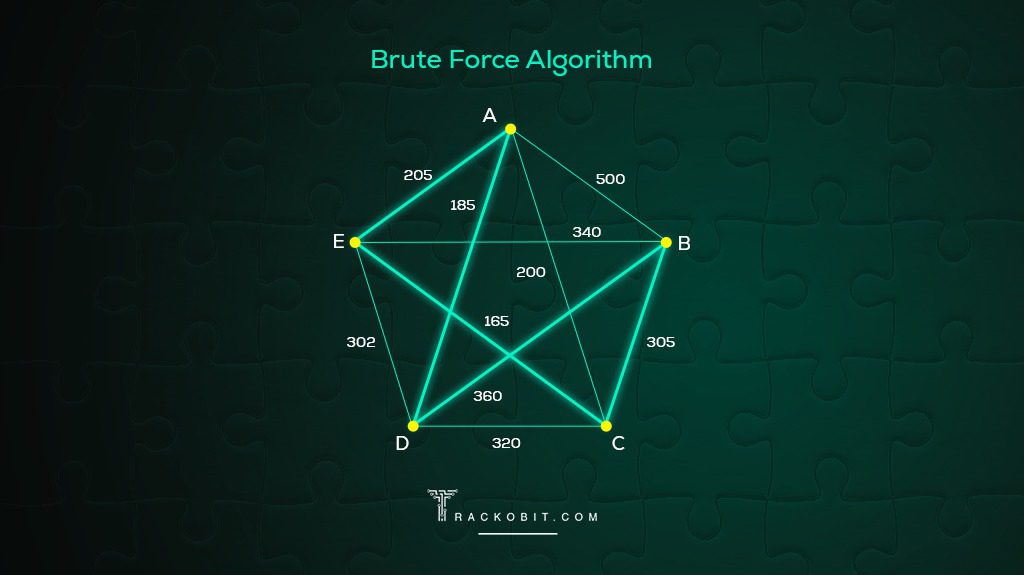
2. Nearest Neighbour Algorithm

The Nearest Neighbour method is the simplest heuristic for the TSP. It starts from the first location and repeatedly selects the closest unvisited location to form a tour. Although it is quick to implement this method, it may always yield the optimal solution for it prioritises proximity over other factors.

Nearest neighbour Algorithm - Traveling Salesman Problem

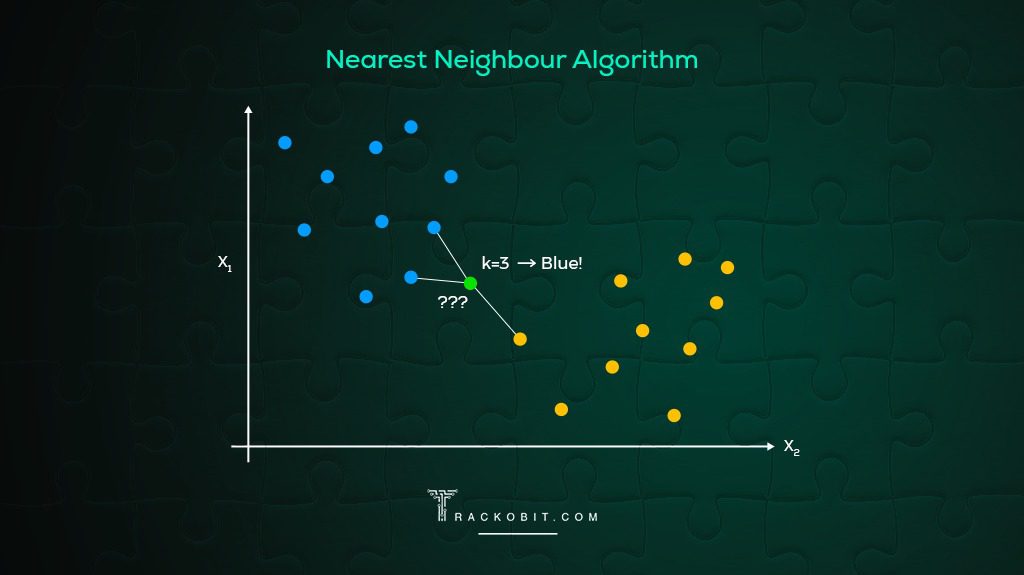
3. Genetic Algorithm

This technique or method draws inspiration from nature itself. They evolve TSP solutions through selection, crossovers and mutation. They pick the best routes and mix them up. This creates new routes that might be even better. Then, they keep the best ones and repeat the mixing and picking process. Survival of the fittest in the true sense.

Genetic Algorithm - Traveling Salesman Problem

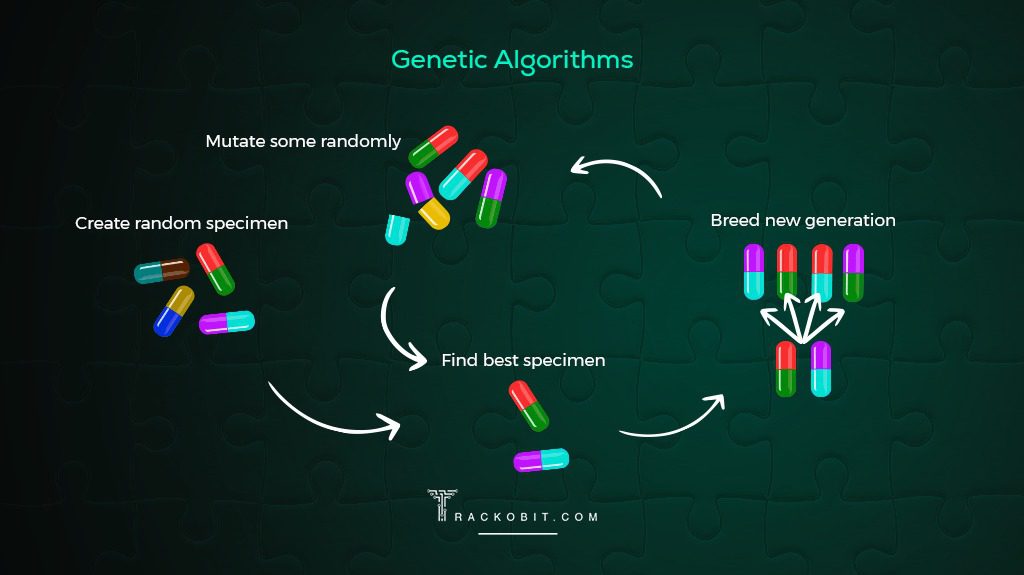
4. Ant Colony Optimisation (ACO)

Ants have a tendency to leave pheromones on the shorter routes they find, calling fellow ants on the same route. They keep leaving more pheromones on the shorter routes they find. Over time, the collective behaviour of the ants causes them to converge on the shortest route. Inspired by the nature of ants, ACO finds the shortest route by analysing the trails of data left by artificial ants based on the strength of these data trails.

Ant Colony Optimisation (ACO) - Traveling Salesman Problem

5. Dynamic Programming

Dynamic Programming is like solving a puzzle, step-by-step, by breaking it into smaller pieces. In TSP challenges, it finds the best route to visit all locations. It begins with figuring out the shortest route between two locations; then it builds on that to find ways to more locations. It’s a smart TSP solution for small scenarios but may require significant memory resources for larger and more complex problems.

What Are Real-world Travelling Salesman Problem Applications?

The Traveling Salesman Problem (TSP) has a wide array of applications across various domains due to its relevance in optimising routes and sequences. Here are several crucial real-word TSP applications and implementations in the real world.

1. TSP implementation in Logistics and Delivery Services

The logistics and supply chain sectors have the widest TSP applications.

Courier, Express & Parcel : Companies like FedEx, UPS, and DHL rely on TSP algorithms to optimise delivery routes for their fleet of delivery trucks. By finding the most efficient sequence of stops, they minimise fuel consumption , reduce delivery TAT, and save on operational overheads too.
On-demand Delivery : Food delivery companies, instant grocery delivery apps and at-home appointment platforms like Swiggy, BlinkIt and UrbanCompany, respectively, leverage TSP solutions to ensure timely delivery. Enhancing the customer experience and increasing the number of deliveries each rider can make.

2. TSP Applications in Transportation and Urban Planning Waste collection routes, Traffic light synchronisation, optic cable installation, etc. are some areas where TSP Solutions works like a knight in shining armour. Other real-world TSP applications include

Public Transport : City planners and public transport agencies use TSP principles to design bus, tram and train routes that reduce travel for passengers.
Emergency Service Dispatch : Ambulance services, Police PCR vans employ TSP algorithms to dispatch vehicles quickly and efficiently in response to emergency calls. Finding the shortest route to reach the incident location can save lives.
Urban Mobility Solution : In the era of ride-sharing and on-demand mobility apps like Uber, Ola, Lyft, etc., real-world TSP applications become prominent. TSP solutions optimise the route to destinations, ensuring quick and cost-effective transportation.

Other significant real-life applications of the Travelling Salesman Problem are

TSP in Healthcare and Medical Research – for DNA sequencing and understanding genetic patterns and diseases.
TSP in Manufacturing and Production – In circuit board manufacturing and job scheduling of technicians.
TSP in Robotics and Autonomous Vehicles -Self-driving cars and drones use TSP-like algorithms for efficient navigation.

Solving the Travelling Salesman Problem – Last Mile Delivery Route Optimisation

Route optimisation is the key to efficient last-mile delivery . In order to attain flawless route optimisation, the software must solve the traveling salesman problem every step of the way.

Why it’s essential to solve TSP for Last Mile Delivery?

In simple and minimal words, solving TSP problems helps in many ways:

Saves Time : It makes deliveries faster, so your customers get orders sooner.
Customer Satisfaction : Fast deliveries give you an edge over the competition and enhance customer experience too.
Saves Money : It reduces fuel wastage and vehicle wear, making deliveries cheaper.
Environment Friendly : It lowers pollution by using fewer vehicles and shorter routes.
Happy Staff: Drivers and dispatchers have less stress and can finish their work faster.

How do we solve the travelling salesman problem for last-mile delivery?

Solving TSP challenges for Last-mile delivery is like solving a big jigsaw puzzle. There are a hundred thousand addresses to visit daily. The software must find the shortest and most optimised route to them and come back to the starting point at the end.

Our route optimisation software , TrackoMile, leverages capacity management , routing algorithms and robust rule engines to present the most optimal combination of delivery addresses. Thereby giving the most optimally planned routes or trips.
All delivery managers have to do is upload the CSV file of the addresses or integrate TrackoMile to their CRM to fetch the delivery addresses. Now trip allocation, route optimisation, dispatch and everything else happen in a few clicks.
ETA when the delivery is en route, POD when the order is delivered successfully, and trip analysis, are added features to simplify overall operations.

The Vehicle Routing Problem is very similar to TSP, with wide applications in logistics, delivery services and transportation. While TSP focuses on finding the shortest route for a single traveller visiting various locations, VRP deals with multiple vehicles serving multiple customers, considering added constraints like vehicle capacity, TATs and more.

How Can AI Help in Solving Traveling Salesman Problem (TSP)?

AI or Artificial Intelligence are becoming the driving force for business growth across various industrial sectors. AI particularly aids in solving the Traveling Salesman Problem(TSP) in the logistics and delivery sector by employing advanced algorithms and techniques. What are a few tricks up AI’s sleeves that help in automating TSP resolution? Let’s find out!

1. Advanced Algorithms

AI algorithms such as Genetic Algorithms, ACO, simulated annealing and a few others mentioned above, tackle complex Travelling Salesman Problem scenarios.

2. Machine Learning

Gathering information from historical data and optimising routes based on real-time insights is what AI is best for. Machine learning models are trained to adapt to changing conditions, like traffic, weather and delivery constraints, to provide a more accurate plan of action.

3. Parallel Computing

AIi enables the use of a parallel computing process, which means solving multiple segments of TSP simultaneously. This accelerates the problem-solving process for large-scale challenges.

4. Heuristic Improvement

TSP Heuristics powered by AI can groom initial solutions, gradually improving their results over time. These heuristics can be applied iteratively by AI to reach better results.

5. Hybrid Approaches

Applying hybrid algorithms is not a new technique to refine techniques and produce more accurate results. AI on top of it singles out data-oriented combinations that work the best in varied use cases.

Wrapping Up!

The travelling salesman problem’s importance lies in its real-world applications. Whether optimising delivery routes, planning manufacturing processes or organising circuit board drilling, finding the most efficient way to cover multiple locations is crucial to minimise costs and save time.

The TSP problems have evolved over the years, and so have TSP algorithms, heuristics and solutions. With the advent of advanced technologies such as GPS and machine learning, TSP continues to adapt and find new applications in emerging fields, cementing its status as a fundamental problem in optimization theory and a valuable tool for various industries. Mobility automation software like Trackobit, TrackoMile and TrackoField resort to TSP heuristics to solve challenges along the way.

Read Blog – Best Delivery Route Planner Apps for 2023

Traveling Salesman Problem FAQs

What is tsp.

TSP is an abbreviation for Traveling Salesman Problem. It’s the routing problem that deals with finding the shortest route to travel to a combination of locations in the most optimal manner.

Is Travelling Salesman Problem Solvable?

Yes, the Traveling Salesman Problem (TSP) is solvable, but the time to find the solution can grow proportionately with an increase in the number of locations. With the evolution of travelling salesman problem applications, various TSP algorithms and heuristics, their hybrids have also emerged.

Wh at is the objective of TSP?

The objective of the Traveling Salesman Problem (TSP) is to find the shortest possible route that covers all given locations or waypoints and comes back to the starting point with the least resource utilisation.

Diksha Bhandari

Currently creating SaaSy content strategies for TrackoBit and TrackoField, this content professional has dedicated a decade of her life to enriching her portfolio and continues to do so. In addition to playing with words and spilling SaaS, she has a passion for traveling to the mountains and sipping on adrak wali chai.

Author Showcase
All Blog Post

Never Miss a Beat

Related Blog

Top 12 Google Map Alternatives – Offering Precise Navigation

Explore our best picks for 12 free Google map alternatives that offer accurate and secure location and navigational solutions.

Food Delivery Trends to Watch in 2024 & Beyond

Food and technology are both revolving along with consumer demands. Here are some of the food delivery trends to watch in 2024.

Biofuel – An Alternative to Fossil Fuels in Transportation | G20

Transportation industries are moving towards a greener future through the sustainable use of biofuels like Ethanol — discussed in the G20 2023 summit.

Top 10 Navigation Apps for Android and iOS | 2024

Discover the 10 best navigation apps in 2024 that offer personalised navigation just like Sherpas (experienced guides of Himalayan terrain) do.

Thematic Maps An Efficient Way of Mapping Out Business

What are Thematic Maps? Types, Applications And Advantages

Maps have come a long way, and their usage has gone beyond just navigating distances. Thematic maps are now being used to interpret data, gain information, etc.

From a Bachelor Pad to a Multinational Firm: Tracking TrackoBit’s 5-year Journey

“It’s when ordinary people rise above the expectations and seize the opportunity that milestones truly are reached.” – Mike Huckabee

Stay Updated on tech, telematics and mobility. Don't miss out on the latest in the industry.

Thank you for reaching out! We'll speak to you soon.

In the meantime, why not find out more about us, explore our products, or visit our blog?

Cookie Consent

We use cookies to enhance and personalize your browsing experience. By continuing to use our website, you agree to our Privacy Policy.

The travelling salesman problem [and how to solve it]

The Travelling Salesman Problem (TSP) refers to the challenge of finding the shortest route between any multiple stops on a map.

Brendan Tobin , Caroline Hassett

The travelling salesman problem (TSP) refers to the efforts of a door-to-door salesman trying to find the shortest and/or quickest way to serve all of the stops on his list of visits in a given time period (usually a working day).

Although it was once the problem of a salesperson, today there are far more workers that are faced with it. In recent years, the explosion of eCommerce and online shopping has seen more and more deliveries made directly to consumers' homes than ever before. For the delivery drivers, it can mean delivering to over 100 individual locations on any given day.

So, getting the travelling salesman problem solved is mission-critical!

In this article, we’ll look at the problem in a bit more detail, as well as discuss the importance of it for various industries including couriers and last mile carriers. If you are struggling with routing salespeople or delivery teams then we have the solution for you . We’ll also take a look at some of the solutions to the problem and discuss which route optimization software is the most suited to solving your own TSP problem.

In this article you will learn:

What is the travelling salesman problem?

Why the travelling salesman problem is important
Possible solutions to the travelling salesman problem
How to practically address the TSP
How SmartRoutes helps to solve the TSP

The Travelling Salesman Problem (TSP) refers to the challenge of finding the shortest route between any multiple stops on a map. It takes its name from the historical challenge faced by door-to-door salespeople who needed to visit as many potential customers in the shortest time possible to increase their sales numbers.

The TSP has become a renowned algorithmic problem in fields of study such as physics, computer sciences, and latterly in logistics and operations research.

Why is the travelling salesman problem important?

When it comes to business, time is money and no matter what businesses you're in, if it involves travelling between multiple locations by vehicle, you need to ensure that it’s doing so in the most efficient way possible.

Consider this for a minute:

According to Route Consultant , a FedEx Ground Driver in the United States does an average of 100 miles or less per day, and completes between 150-230 stops a day, which includes pickups.

Believe it or not, there are trillions (yes, trillions) of unique ways that each of these stops could be served. Of course, some of these are most obviously not the most efficient routes, but actually determining which one is can be a challenge that is still beyond practical human capabilities.

What began as a field sales problem many moons ago is now a very real issue in the supply chain logistics industry. For any business that has more than a couple of vehicles, ensuring that they are all delivering goods in the most efficient manner can be the difference between having a viable business model, or not.

By attempting to solve the TSP, we can find the most efficient routes for delivery drivers to take when out on the road. This results in less distance being travelled, less fuel being used and fewer hours driven. This means a double bonus for the balance sheet in any delivery-based business operation.

But the travelling salesman problem (TSP) isn’t just important for businesses' financial viability. With the ever-increasing importance of reducing our carbon footprint, reducing the distances travelled directly contributes to the amount of fossil fuels being burned. We all have a part to play, and the ability to effect such important change through problem solving is a bonus for the greater society too. In fact, a recent effort to reduce the time taken for a politician to tour the UK shows how difficult the problem is.

The benefits of solving this problem (TSP) also trickles down to the customers who rely on timely and efficient delivery of goods. Whether they need the deliveries for the operations of their own businesses, or whether they rely on on-time delivery of medication for personal illness, it has real-world implications for everyone that relies on it. Believe it or not, customer experience (or as it’s correctly termed in the last mile, ‘delivery experience’) is another big reason why the TSP is so important.

SmartRoutes Route Planning Software

Streamline your entire delivery process, all from one platform

Try it for free today

Delivery man cross checking the order details on the package and the delivery management system

Possible solutions to the Travelling Salesman Problem

There are literally entire books dedicated to trying to solve the TSP , so it is important to note that what we list below are ‘possible’ solutions rather than ‘actual solutions’. The TSP is what is referred to as a ‘NP-hard’ problem, which means that there literally is no known solution to it.

However, some of the more notable or practical answers to the problem are as follows:

1. The ‘Brute-Force’ check

The trouble with the travelling salesman problem (TSP), is that technically, it is solvable. You just need to work out every possible sequence that a number of stops can be served. Right?

Well, sure, but the number of routes possible grows so rapidly that even the most powerful of modern algorithmic computers fail at the task. The trouble with creating an optimized route for 10 stops isn’t the problem per se, it’s creating the route fast.

Well, this is what the brute-force method attempts, or as it’s also known, the ‘naive approach’. It calculates all the possible permutations, finds the shortest one possible and then selects the route that is actually the shortest.

2. The branch and bound approach

The branch and bound approach pays attention to finding the lowest possible cost for the remaining pathways that the initial stages of approaches like the brute-force provide.

Sometimes referred to as Parallel TSP , it assumes that we don’t want to try every single ‘possible’ route. Even using common sense, would probably narrow it down somewhat. For example, we’re not going to go to the furthest drop-off point first and then return to the one nearest to the depot. By using nodes, and attaching ‘costs’ to each node, the algorithm estimates how likely a given choice is to lead to a solution to the problem.

3. The Nearest Neighbour Method

With the nearest neighbour approach, the algorithm begins with the start location of the route, and then adds the stop nearest to it. A list of locations visited is already served, and if a stop has been served it is skipped and the next stop is added. Once the final stop is reached, you return to the start location again.

The benefit of the nearest neighbour method is that it is relatively quick to do, and also more practical than the other 2 approaches outlined. The downside, however, is that it isn't always as accurate at providing the optimized route as the other two approaches.

How to practically address the travelling salesman problem

Well, if you’ve managed to read this far, you know that the answer is unsolvable in a literal sense but in a practical sense, it is!

While algorithms might not give you the very quickest or cheapest route every single time, they can do so much more effectively than the human brain can. As we’ve seen with the nearest neighbour method, it is possible to use computational power to automatically eliminate the bulk of routes that would most obviously not be efficient. Furthermore, the same computers can also then select which route is the quickest (or in mathematical terms has the lowest cost) from the remaining options.

As technology advances, and machine learning and automation become more powerful than ever, route planning and optimization can be done in a matter of seconds. There are essentially two processes that are complete: the mathematical equation and the automated selection of the best route. This has been a game changer for the road transport industry, particularly with larger volumes of packed goods being distributed in smaller quantities in recent years.

How SmartRoutes Solves the Travelling Salesman Problem

SmartRoutes is what is referred to as delivery management software. As a total delivery software solution, it helps businesses to manage everything from order management and fulfilment, to the planning of routes for delivery drivers and the capture of proof-of-delivery for end customers.

At the core of the solution, however, is route optimization . This means that we have developed the solution with on clear overall aim:

To create the quickest and most efficient routes for delivering goods by road as quickly as is technically possible.

Now as we’ve discussed, there isn't a cut-and-dry solution to the travelling salesman problem. But here at SmartRoutes, we took what is regarded as the best approach, added the best technology and then set about accounting for every other factor that plays a role in the delivery of goods by delivery vehicles.

Some of the most obvious ones include the size of fleets, the types of roads, real-time driver analytics, and whether time or distance between stops is a better indicator of efficiency based on field-testing.

However, we have also accounted for some less obvious factors in our own algorithm. For example, our algorithm is weighted to prefer routes that have less right turns for users in the US and the UK.

Why? Well, because crossing traffic is actually a time-suck when it comes to delivering large volumes of goods. By turning left, drivers don’t have to wait for oncoming traffic to pass before continuing their route. Of course, this is also much safer for drivers which is another reason why we adopted this within our routing algorithm.

If you're looking to create a great delivery experience for your customers then look no further than SmartRoutes. You can try it out with our 7-day free trial or book a demo today. We can get you up and running in minutes and help you to make the most of it from the outset.

Frequently asked questions

1. what is the traveling salesman problem (tsp), and why is it important.

The traveling salesman problem (TSP) is a classic optimization problem in which a salesperson must find the shortest possible route that visits a set of given cities exactly once and returns to the starting city. It's important because it has applications in various fields like logistics, transportation, and manufacturing, where efficient routing and cost-saving are crucial.

2. Are there practical applications of TSP-solving algorithms?

Yes, TSP-solving algorithms have numerous practical applications. For instance, they are used in optimizing delivery routes for couriers and delivery services, planning circuit design on computer chips, and even in DNA sequencing.

3. What are some common algorithms to solve the traveling salesman problem?

Brute-Force Method: Exhaustively explores all possible routes.
Nearest Neighbour: Select the nearest unvisited city at each step.
The Branch and Bound Approach: This pays attention to finding the lowest possible cost for the remaining pathways.

4. What are the limitations and challenges associated with solving the traveling salesman problem?

Solving the TSP can be challenging due to its computational complexity. As the number of cities increases, the problem becomes exponentially harder to solve. Additionally, approximating an optimal solution for large datasets can be time-consuming. Researchers are continually working on algorithms to address these challenges and find efficient solutions for real-world TSP instances.

If you enjoyed this blog, you might also be interested in:

Customer stories
What's New!
Integrations
Route planning
Route optimization
Delivery fleet tracking
Customer experience
Proof of delivery
Delivery driver app
Order management
Terms & Privacy

A concise guide to the Traveling Salesman Problem

Special Issue Paper
Published: 30 November 2009
Volume 61 , pages 35–40, ( 2010 )

Cite this article

G Laporte 1

697 Accesses

57 Citations

1 Altmetric

Explore all metrics

The Traveling Salesman Problem ( TSP ) is one of the most famous problems in combinatorial optimization. Hundreds of papers have been written on the TSP and several exact and heuristic algorithms are available for it. Their concise guide outlines the most important and best algorithms for the symmetric and asymmetric versions of the TSP. In several cases, references to publicly available software are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Applegate DL, Bixby RE, Chvátal V and Cook WJ (2003). Implementing the Dantzig–Fulkerson–Johnson algorithm for large scale traveling salesman problems . Math Program Ser B 97: 91–153.

Google Scholar

Applegate DL, Bixby RE, Chvátal V and Cook WJ (2006). The Traveling Salesman Problem: A Computational Study . Pinceton Series in Applied Mathematics: Princeton.

Applegate DL, Bixby RE, Chvátal V, Cook WJ, Espinoza DG, Goycoolea M and Helsgaun K (2009). Certification of an optimal TSP tour through 85900 cities . Opns Res Lett 37: 11–15.

Article Google Scholar

Babin G, Deneault S and Laporte G (2007). Improvements to the Or-opt heuristic for the symmetric travelling salesman problem . J Opl Res Soc 58: 402–407.

Balas E and Toth P (1985). Branch and bound methods . In: Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester, pp. 361–401.

Burkard R, Dell'Amico M and Martello S (2009). Assignment Problems . SIAM: Philadelphia.

Book Google Scholar

Carpaneto G and Toth P (1980). Some new branching and bounding criteria for the asymmetric traveling salesman problem . Mngt Sci 26: 736–743.

Carpaneto G and Toth P (1987). Primal-dual algorithms for the assignment problem . Discrete Appl Math 18: 137–153.

Carpaneto G, Dell'Amico M and Toth P (1995). Exact solution of large-scale, asymmetric travelling salesman problems . ACM Trans Math Software 21: 394–409.

Chvátal V (1973). Edmonds polytopes and weakly Hamiltonian graphs . Math Program 5: 29–40.

Cornuéjols G, Fonlupt J and Naddef D (1985). The travelling salesman problem on a graph and some related integer polyhedra . Math Program 33: 1–27.

Croes GA (1958). A method for solving large scale symmetric traveling salesman problems . Opns Res 6: 791–812.

Crowder H and Padberg MW (1980). Solving large-scale symmetric traveling salesman problems to optimality . Mngt Sci 26: 495–509.

Daganzo CF (1984). The length of tours in zones of different shapes . Transport Res B 18: 135–145.

Dantzig GB, Fulkerson DR and Johnson SM (1954). Solution of a large-scale traveling-salesman problem . Opns Res 2: 393–410.

Dell'Amico M and Toth P (2000). Algorithms and codes for dense assignment problems: The state of the art . Discrete Appl Math 100: 17–48.

Eastman WL (1958). Linear programming with pattern constraints. PhD thesis, Department of Economics, Harvard University, Cambridge, MA.

Edmonds J (1965). Maximum matching and a polyhedron with 0,1-vertices . J Res Natl Bur Stan 69B: 125–130.

Fischetti M and Toth P (1992). An additive bounding procedure for the asymmetric traveling salesman problem . Math Program Ser A 53: 173–197.

Fischetti M, Lodi A and Toth P (2002). Exact methods for the asymmetric traveling salesman problem . In: Gutin G and Punnen AP (eds). The Traveling Salesman Problem and Its Variations. Kluwer: Boston, pp. 169–205.

Flood MM (1956). The traveling-salesman problem . Opns Res 4: 61–75.

Gaboune B, Laporte G and Soumis F (1994). Optimal strip sequencing strategies for flexible manufacturing operations in two and three dimensions . Int J Flex Manuf Sys 6: 123–135.

Golden BL and Stewart WR (1985). Empirical analysis of heuristics . In: Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester, pp. 207–249.

Gomory RE (1963). An algorithm for integer solutions to linear programs . In: Graves RL and Wolfe P (eds). Recent Advances in Mathematical Programming. McGraw-Hill: New York, pp. 269–302.

Grötschel M and Holland O (1991). Solution of large-scale symmetric traveling salesman problems . Math Program 51: 141–202.

Grötschel M and Padberg MW (1985). Polyhedral theory . In: Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester, pp. 251–305.

Grötschel M and Pulleyblank WR (1986). Clique tree inequalities and the symmetric Travelling Salesman Problem . Math Opns Res 11: 537–569.

Gutin G and Punnen AP (eds) (2002). The Traveling Salesman Problem and Its Variations. Kluwer: Boston.

Held M and Karp RM (1971). The traveling-salesman problem and minimum spanning trees: Part II . Math Program 1: 6–25.

Helsgaun K (2000). An effective implementation of the Lin–Kernighan traveling salesman heuristic . Eur J Opl Res 126: 106–130.

Johnson DS, Gutin G, McGeoch LA, Yeo A, Zhang W and Zverovitch A (2002). Experimental analysis of heuristics for the ATSP . In: Gutin G and Punnen AP (eds). The Traveling Salesman Problem and Its Variations. Kluwer: Boston, pp. 445–487.

Johnson DS and McGeoch LA (1997). The traveling salesman problem: A case study . In: Aarts E and Lenstra JK (eds). Local Search in Combinatorial Optimization. Wiley: Chichester, pp. 215–310.

Johnson DS and McGeoch LA (2002). Experimental analysis of heuristics for the STPS . In: Gutin G and Punnen AP (eds). The Traveling Salesman Problem and Its Variations. Kluwer: Boston, pp. 369–443.

Jünger M, Reinelt G and Rinaldi G (1995). The traveling salesman problem . In: Ball MO, Magnanti TL, Monma CL and Nemhauser GL (eds). Network Models Handbooks in Operations Research and Management Science vol. 7. North-Holland: Amsterdam, pp. 225–330.

Karp RM (1979). A patching algorithm for the nonsymmetric traveling-salesman problem . SIAM J Comput 8: 561–573.

Karp RM and Steele JM (1985). Probabilistic analysis of heuristics . In: Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester, pp. 181–205.

Land AH (1979). The solution of some 100-city traveling salesman problems. Technical report, London School of Economics, London.

Land AH and Doig AG (1960). An automatic method of solving discrete programming problems . Econometrica 28: 497–520.

Laporte G (1992). The traveling salesman problem: An overview of exact and approximate algorithms . Eur J Opl Res 59: 231–247.

Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds) (1985). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester.

Lin S (1965). Computer solutions of the traveling salesman problem . Bell Syst Tech J 44: 2245–2269.

Lin S and Kernighan BW (1973). An effective heuristic algorithm for the traveling salesman problem . Opns Res 21: 498–516.

Little JDC, Murty KG, Sweeney DW and Karel C (1963). An algorithm for the traveling salesman problem . Opns Res 11: 972–989.

Martin GT (1966). Solving the traveling salesman problem by integer programming. Working Paper, CEIR, New York.

Miliotis P (1976). Integer programming approaches to the travelling salesman problem . Math Program 10: 376–378.

Miliotis P (1978). Using cutting planes to solve the symmetric travelling salesman problem . Math Program 15: 177–188.

Naddef D (2002). Polyhedral theory and branch-and-cut algorithms for the symmetric TSP . In: Gutin G and Punnen AP (eds). The Traveling Salesman Problem and Its Variations. Kluwer: Boston, pp. 29–116.

Öncan T, Altınel IK and Laporte G (2009). A comparative analysis of several asymmetric traveling salesman problem formulations . Comput Opns Res 36: 637–654.

Or I (1976). Traveling salesman-type combinatorial problems and their relation to the logistics of regional blood banking. PhD thesis, Department of Industrial Engineering and Management Sciences, Northwestern University, Evanston, Il.

Orman AJ and Williams HP (2006). A survey of different integer programming formulations of the travelling salesman problem . In: Kontoghiorghes E and Gatu C (eds). Optimisation, Econometric and Financial Analysis Advances in Computational Management Science. Springer: Berlin, Heidelberg, pp. 91–104.

Padberg MW and Grötschel M (1985). Polyhedral computations . In: Lawler EL, Lenstra JK, Rinnooy Kan AHG and Shmoys DB (eds). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. Wiley: Chichester, pp. 307–360.

Padberg MW and Hong S (1980). On the symmetric travelling salesman problem: A computational study . Math Program Study 12: 78–107.

Padberg MW and Rinaldi G (1987). Optimization of a 532-city symmetric traveling salesman problem by branch and cut . Opns Res Lett 6: 1–7.

Padberg MW and Rinaldi G (1991). A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems . SIAM Rev 33: 60–100.

Toth P and Vigo D (eds) (2002). The Vehicle Routing Problem. SIAM Monographs on Discrete Mathematics and Applications, Philadelphia.

Download references

Acknowledgements

This research was partially supported by the Canadian Natural Sciences and Engineering Research Council under grant 39682-05. This support is gratefully acknowledged. Thanks are due to a referee who provided valuable comments.

Author information

Authors and affiliations.

Canada Research Chair in Distribution Management, HEC Montréal, Canada

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G Laporte .

Rights and permissions

Reprints and permissions

About this article

Laporte, G. A concise guide to the Traveling Salesman Problem. J Oper Res Soc 61 , 35–40 (2010). https://doi.org/10.1057/jors.2009.76

Download citation

Received : 01 April 2009

Accepted : 01 May 2009

Published : 30 November 2009

Issue Date : 01 January 2010

DOI : https://doi.org/10.1057/jors.2009.76

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Traveling Salesman Problem
exact algorithms
Find a journal
Publish with us
Track your research

The Geography of Transport Systems

The spatial organization of transportation and mobility

The Traveling Salesperson Problem

The “traveling salesperson” problem is a classic route selection problem where a sequence of locations has to be traveled to, and a return must be made to the starting location. Each location can only be traveled once. In the above example, a salesperson, starting at point 1, must visit six locations (1 to 6) and return to the starting point. The first route (1-4-2-5-6-3-1), with a total length of 62 km, is an acceptable solution but not the best. The second route (1-2-5-4-6-3-1) represents a much better solution as the total distance, 48 km, is less than the first route. This example assumes Euclidean distances and an isotropic space, but in reality, the solution may be different considering the configuration of transport infrastructures, making some locations more accessible than others. These types of problems are usually solved through combinational optimization, which is a branch of operations research.

The Travelling Salesman Problem in Artificial Intelligence – Strategies, Solutions, and Future Directions

The Travelling Salesman Problem (TSP) is a classic challenge in computer science and optimization. It involves finding the shortest possible route for a salesman or salesperson to travel between a set of cities, visiting each city exactly once and returning to the starting city. This problem has numerous real-life applications, such as route planning for delivery drivers, scheduling for sales representatives, and optimizing circuit board designs.

Artificial Intelligence (AI) techniques have proven to be incredibly effective in solving complex problems like the TSP. By leveraging the power of machine learning algorithms and advanced optimization techniques, researchers have developed intelligent approaches to tackle this challenging problem. These AI techniques not only provide optimal solutions but also significantly reduce the computation time required to solve large-scale instances of the TSP.

One popular AI technique used to solve the TSP is the use of genetic algorithms. These algorithms mimic the process of natural selection and evolution to generate a set of candidate solutions, and then iterate and refine these solutions over multiple generations. With each iteration, the genetic algorithm applies genetic operators, such as crossover and mutation, to create new, potentially better solutions. The algorithm evaluates the fitness of each solution based on the distance traveled and selects the best solutions to form the next generation. Through this iterative process, the genetic algorithm gradually converges towards an optimal solution for the TSP.

Another AI technique that has shown promise in solving the TSP is the use of reinforcement learning. Reinforcement learning is a type of machine learning where an agent learns to make decisions based on feedback from its environment. In the context of the TSP, the agent learns to select the next city to visit based on the current state of the solution. Through trial and error, the agent discovers the optimal sequence of cities to visit, resulting in the shortest possible route for the salesman. By using techniques such as deep Q-learning, researchers have achieved impressive results in solving the TSP, even for large problem instances.

Travelling Salesman Problem Explained

The Travelling Salesman Problem (TSP) is a well-known problem in the field of artificial intelligence and operations research. It is a classic combinatorial optimization problem that involves finding the shortest possible route for a salesperson to travel to a number of cities and return back to the starting city, visiting each city only once.

In the TSP, a salesperson is given a list of cities and the distances between each pair of cities. The goal is to find a route that minimizes the total distance traveled. This problem is NP-hard, which means that as the number of cities increases, the amount of time it takes to solve the problem grows exponentially.

There are various algorithms that have been developed to solve the TSP, ranging from exact algorithms that guarantee finding the optimal solution, to heuristic algorithms that provide near-optimal solutions. Some of the popular techniques used to solve the TSP include genetic algorithms, simulated annealing, and ant colony optimization.

Artificial Intelligence and the TSP

Artificial intelligence (AI) techniques have been widely used to solve the TSP. These techniques not only provide efficient solutions but also allow for the exploration of large search spaces. Machine learning, in particular, has been utilized to learn patterns and generate solutions to the TSP. By training machine learning models on large datasets, it is possible to find solutions that are close to optimal or even optimal in some cases.

AI algorithms can be used to find solutions to the TSP in real-time by taking into account various factors such as traffic conditions, time constraints, and cost optimization. These algorithms can be integrated into navigation systems or logistics planning tools to help salespersons and logistics coordinators optimize their routes and minimize their travel time.

The Travelling Salesman Problem is a complex problem in the field of artificial intelligence and operations research. It involves finding the shortest possible route for a salesperson to travel to a number of cities and return back to the starting city. AI techniques, such as machine learning, have been utilized to solve the TSP and find near-optimal solutions. These solutions can be used to optimize travel routes and minimize travel time for salespersons and logistics coordinators.

By leveraging the power of AI, the TSP can be efficiently solved, leading to improved efficiency and cost savings in various industries that require optimal route planning.

Importance of Solving the TSP

The Travelling Salesman Problem (TSP) is a classic problem in the field of artificial intelligence and machine learning. It is a mathematical problem that involves finding the shortest possible route between a set of cities, with the constraint that each city must be visited exactly once and the salesman must return to the starting city.

Solving the TSP is important for various reasons. Firstly, it has practical applications in various industries such as logistics and transportation. For example, a salesperson visiting multiple cities needs to find the most efficient route to minimize travel time and expenses. By solving the TSP, companies can optimize their routes and save resources.

Secondly, solving the TSP has significant theoretical implications. It is classified as an NP-hard problem, which means that finding the optimal solution becomes exponentially difficult as the size of the problem increases. Therefore, developing efficient algorithms to solve the TSP contributes to the advancement of algorithms and complexity theory.

Moreover, solving the TSP can lead to insights and improvements in other optimization problems. Many problems in various domains can be reduced to the TSP, allowing researchers to apply TSP-solving techniques to solve other complex problems more effectively.

Overall, the TSP is not only a challenging problem in itself but it also has practical and theoretical importance. Solving the TSP using artificial intelligence techniques can lead to more efficient routes, cost savings, and advancements in algorithmic research.

Artificial Intelligence Techniques for Solving TSP

The Traveling Salesman Problem (TSP) is a well-known optimization problem in computer science and operations research. It involves finding the shortest possible route that a salesperson must take to visit a set of cities and return to the starting city, while visiting each city only once.

Artificial Intelligence (AI) techniques have been widely used to tackle the TSP and find near-optimal solutions. These techniques leverage the power of machine learning and optimization algorithms to solve the problem efficiently and effectively.

1. Genetic Algorithms

Genetic algorithms are a popular AI technique for solving the TSP. They mimic the process of natural selection, where a population of potential solutions evolves over time to find the optimal solution. In the context of the TSP, each individual in the population represents a possible tour, and the fitness of the tour is evaluated based on its length. Through the use of genetic operators, such as mutation and crossover, the algorithm explores different combinations of tours to converge towards the shortest route.

2. Ant Colony Optimization

Ant Colony Optimization (ACO) is another AI technique that has been successfully applied to the TSP. Inspired by the behavior of real ants searching for food, ACO algorithms simulate the movement of artificial ants on a graph representing the cities. Each ant probabilistically chooses its next move based on pheromone trails left by other ants and the distance to the neighboring cities. Over time, the pheromone trails are updated based on the quality of the tours, allowing the algorithm to discover better routes.

These are just two examples of the many AI techniques that have been employed to solve the TSP. Other techniques, such as simulated annealing, particle swarm optimization, and reinforcement learning, have also been used with success. Each technique offers its own advantages and trade-offs in terms of solution quality, runtime, and scalability.

In conclusion, artificial intelligence techniques provide powerful tools for solving the TSP. These techniques leverage the intelligence and learning capabilities of machines to explore the vast search space of possible tours and find near-optimal solutions. By combining different AI techniques and tailoring them to the specific problem instance, researchers and practitioners can tackle the TSP efficiently and effectively.

Genetic Algorithms for TSP

Genetic Algorithms (GAs) have been widely used to solve complex optimization problems, including the Traveling Salesman Problem (TSP). The TSP is a classic problem in the field of artificial intelligence, where a salesman or salesperson needs to visit a set of cities and return to the starting point while minimizing the total distance traveled.

GAs are a type of machine learning algorithm inspired by the process of natural selection. They work by evolving a population of potential solutions through generations, mimicking the process of evolution in nature. In the context of the TSP, each potential solution represents a possible route that the salesman can take to visit all the cities.

The GA starts by randomly generating an initial population of potential solutions, also known as individuals or chromosomes. Each individual is represented as a sequence of cities, encoding a possible route for the salesman. The fitness of each individual is then calculated based on the total distance of the route. The goal of the GA is to find the individual with the shortest distance, representing the optimal solution to the TSP.

During each iteration, the GA selects individuals from the population to undergo genetic operations such as crossover and mutation. Crossover involves combining the genetic material of two individuals to create new offspring, while mutation introduces small random changes to the genetic material of an individual. These operations help explore the search space and potentially find better solutions.

After the genetic operations, a new population is created using the offspring and a selection process, where individuals with higher fitness have a higher chance of being selected. This process is repeated for a fixed number of generations or until a stopping criterion is met, such as reaching a satisfactory solution.

The use of GAs for solving the TSP has been successful, as they can efficiently explore the vast search space of possible routes and converge to near-optimal solutions. However, the performance of GAs can be affected by various factors, such as the population size, selection method, and genetic operators. Parameters need to be carefully tuned to achieve good results.

In summary, Genetic Algorithms provide an effective approach to solving the Traveling Salesman Problem and have been applied successfully in various real-world scenarios. Their ability to explore the search space and find near-optimal solutions makes them a valuable tool in the field of artificial intelligence and optimization.

Ant Colony Optimization for TSP

Ant Colony Optimization (ACO) is a metaheuristic algorithm inspired by the behavior of ants in finding the shortest paths between their nest and food sources. It has been successfully applied to solve the Traveling Salesperson Problem (TSP), which is a classic optimization problem in computer science.

The TSP involves finding the shortest route that a salesperson can take to visit a given set of cities and return to the starting city, having visited each city only once. The problem is NP-hard, meaning that it becomes computationally infeasible for large problem instances. ACO is an intelligent technique that provides a good approximation solution to the TSP.

How does ACO work?

In ACO, a population of artificial ants are used to find near-optimal solutions to the TSP. Each ant constructs a solution by probabilistically choosing the next city to visit based on a combination of pheromone trails and distance information. Pheromone trails represent the accumulated historic information about good routes, and evaporation and reinforcement mechanisms are used to update the pheromone trail strengths.

During the construction of solutions, ants deposit pheromone on the edges they traverse, with stronger pheromone concentration on shorter edges. This pheromone trail guides subsequent ants to select edges with higher pheromone concentration, increasing the likelihood of finding shorter routes. The pheromone trails also gradually evaporate over time, allowing exploration of new routes.

Benefits of ACO for TSP

ACO offers several advantages for solving the TSP:

Efficiency: ACO is capable of producing good-quality solutions to large-scale TSP instances in a reasonable amount of time, outperforming many other traditional optimization algorithms.
Scalability: ACO scales well with the problem size, making it suitable for solving real-world TSP instances with a large number of cities.
Adaptability: ACO is adaptable to dynamic TSP instances, as it can quickly react to changes in the problem by updating the pheromone trails.

Overall, ACO has proven to be a powerful technique for solving the TSP, providing solutions that are close to the optimal ones. Its ability to leverage the collective intelligence of a population of artificial ants makes it a popular choice in the field of artificial intelligence and machine learning.

Simulated Annealing for TSP

The Travelling Salesman Problem (TSP) is a classic problem in the field of artificial intelligence and machine learning. It involves finding the most efficient route that a salesperson can take to visit a given set of cities and return to the starting city, while minimizing the total distance traveled.

Simulated annealing is a metaheuristic algorithm that is often used to solve optimization problems like the TSP. It is inspired by the annealing process in metallurgy, where a material is heated and slowly cooled to reduce its defects and increase its strength.

In the context of the TSP, simulated annealing works by iteratively improving a solution while allowing for occasional “worse” moves, in order to explore the solution space and avoid getting stuck in local optima. The algorithm starts with an initial solution and iteratively adjusts it by swapping two cities in the tour. Whether or not a new solution is accepted depends on its cost and a temperature parameter, which controls the likelihood of accepting worse solutions as the algorithm progresses.

At each iteration, the temperature is decreased, simulating the cooling process in annealing. This allows the algorithm to explore a larger portion of the solution space in the beginning, and gradually focus on areas with lower costs as the temperature decreases. The cooling schedule is an important parameter that affects the algorithm’s performance, as a schedule that cools too quickly may result in premature convergence to a suboptimal solution.

Simulated annealing for the TSP has been widely studied and proven to be effective in finding near-optimal solutions for large problem instances. Various strategies for generating initial solutions and updating the temperature schedule have been proposed, and the algorithm has been combined with other techniques such as local search and genetic algorithms to further improve its performance.

In conclusion, simulated annealing is an effective technique for solving the Travelling Salesman Problem. It utilizes the concept of annealing to explore the solution space and find near-optimal solutions. By allowing for occasional “worse” moves, it avoids getting stuck in local optima and provides a good balance between exploration and exploitation. With appropriate parameter tuning, simulated annealing can offer high-quality solutions for large-scale TSP instances.

Tabu Search for TSP

Travelling Salesman Problem (TSP) is a well-known optimization problem in the field of artificial intelligence and machine learning. It involves finding the shortest possible route that a salesperson can take to visit a given set of cities and return to the starting city. TSP is known to be a difficult problem and has been extensively studied due to its practical applications in logistics, routing, and planning.

One of the popular approaches to solve TSP is using the Tabu Search algorithm. Tabu Search is a metaheuristic algorithm that is inspired by the concept of memory in human cognition. The algorithm maintains a memory structure called the “tabu list” to keep track of recently visited solutions and prevents the search from getting trapped in repetitive cycles.

How Tabu Search works for TSP

The Tabu Search algorithm for TSP starts with an initial random solution or a known good solution. It then iteratively explores the solution space by making small modifications to the current solution. These modifications are guided by certain rules and heuristics, and new solutions are evaluated based on a cost function that measures the length of the tour.

The algorithm maintains a tabu list that stores recently visited solutions and prevents revisiting them in subsequent iterations. This helps the algorithm to escape local optima and explore new regions of the solution space. Additionally, the algorithm uses a strategy called “aspiration criteria” that allows revisiting a solution in the tabu list if it leads to a better solution than the current best solution.

The Tabu Search algorithm continues the search until a termination criterion is met, such as reaching a predefined number of iterations or a specific improvement threshold. The best solution found during the search is then returned as the final solution to the TSP problem.

Benefits of using Tabu Search for TSP

Tabu Search has several advantages when applied to the Travelling Salesman Problem:

It is a versatile and flexible algorithm that can handle TSP instances of various sizes and complexities.
Tabu Search is able to escape local optima and converge towards good quality solutions.
It can be easily combined with other optimization techniques and heuristics to further improve the solution quality.

In conclusion, Tabu Search is an effective and popular algorithm for solving the Travelling Salesman Problem. Its ability to explore the solution space while avoiding repetitive cycles makes it a valuable tool in the field of artificial intelligence and machine learning.

Particle Swarm Optimization for TSP

The Travelling Salesman Problem (TSP) is a classic optimization problem in the field of artificial intelligence (AI). It involves finding the shortest possible route that a salesperson can take to visit a set of cities and return to the starting city. TSP is a challenging problem that has applications in logistics, transportation, and many other fields.

One popular technique for solving TSP is Particle Swarm Optimization (PSO). PSO is a population-based optimization algorithm inspired by the behavior of bird flocking or fish schooling. In PSO, a set of particles move through the problem’s solution space, searching for the optimal solution.

Each particle in the swarm represents a potential solution to the TSP problem. The particles move towards better solutions by adjusting their positions based on their own best solution and the best solution found by the swarm so far. This enables the particles to explore the search space efficiently and converge towards a good solution.

The optimization process in PSO involves iterating through multiple generations of particles. In each iteration, the particles evaluate their positions using a fitness function that measures the quality of their solutions. The fitness function for TSP typically calculates the total distance travelled by the salesperson.

Advantages of PSO for TSP

PSO has several advantages for solving the TSP:

PSO is a global optimization algorithm, meaning it is able to find the global optimum rather than getting stuck in local optima.
PSO is a population-based algorithm, allowing multiple solutions to be explored concurrently.
PSO can handle TSP instances with a large number of cities efficiently.
PSO is easy to implement and tune for different TSP instances.

Limitations of PSO for TSP

Despite its advantages, PSO also has some limitations when applied to the TSP:

PSO may require a large number of particles to find good solutions for complex TSP instances.
PSO may converge prematurely to suboptimal solutions.
PSO performance can be sensitive to the choice of parameters, such as the swarm size and velocity update equations.

In conclusion, Particle Swarm Optimization is a powerful technique for solving the TSP, leveraging AI and optimization principles. It offers advantages like global optimization and population-based search, but also has some limitations. When applied correctly and fine-tuned, PSO can provide efficient and effective solutions to the TSP.

Neural Networks for TSP

The Traveling Salesman Problem (TSP) is a well-known problem in the field of artificial intelligence and machine learning. It involves finding the shortest possible route that a salesperson can take to visit a given set of cities and return to the starting city. TSP is known to be an NP-hard problem, meaning that finding the optimal solution becomes exponentially difficult with an increase in the number of cities.

Artificial neural networks (ANN) have been widely used to solve TSP due to their ability to learn complex patterns and relationships. ANN is a computational model inspired by the human brain, consisting of interconnected nodes, or artificial neurons, that process and transmit information. By training the neural network on a set of training data, it can learn the optimal routes for different instances of the TSP problem.

There are several approaches to using neural networks for solving TSP. One common method is to represent the TSP problem as a graph, where the cities are nodes and the distances between them are edges. The neural network is then trained to predict the optimal route by adjusting the weights of its connections. Another approach is to use a recurrent neural network (RNN) that takes into account the order in which the cities are visited, as the order can greatly affect the total distance traveled.

Benefits of using neural networks for solving TSP

Using neural networks for TSP has several advantages. Firstly, neural networks can handle large amounts of data and complex relationships, making them suitable for solving the TSP problem with a large number of cities. Secondly, neural networks can be trained on a variety of inputs and can generalize their learning to solve TSP instances that were not part of the training set. This makes them more flexible and adaptable compared to traditional algorithms for TSP.

Challenges and future directions

Despite the benefits, there are some challenges in using neural networks for TSP. The main challenge is the training process, as it requires a large amount of training data and computational resources. Additionally, finding the optimal architecture and parameters for the neural network can be a challenging task in itself.

Future research directions for using neural networks in solving TSP include developing more efficient training algorithms, exploring different network architectures, and integrating other optimization techniques with neural networks. The goal is to further improve the performance and efficiency of neural network approaches in solving the TSP problem and pave the way for more effective AI-based solutions in the field of traveling salesman problem.

Machine Learning Approaches for TSP

The Traveling Salesman Problem (TSP) is a classic optimization problem in artificial intelligence (AI) that involves finding the shortest possible route for a salesperson to visit a given set of cities and return to the starting point. This problem is known to be NP-hard, which means that finding the optimal solution becomes computationally expensive as the number of cities increases.

In recent years, machine learning has emerged as a powerful tool for solving complex problems like the TSP. Researchers have developed various approaches using AI techniques to tackle the TSP and improve upon traditional optimization algorithms. These machine learning approaches aim to find approximate solutions that are close to the optimal solution while reducing the computational burden.

Reinforcement Learning

One popular approach for solving TSP using machine learning is reinforcement learning (RL). RL is a type of AI technique where an agent learns to make decisions by interacting with an environment and receiving rewards or penalties based on its actions. In the context of TSP, the agent can be trained to learn a policy that guides it in choosing the next city to visit. The agent takes into account the current city, the remaining cities, and the distances between them to make the decision. Through trial and error, the agent improves its policy to find better and better solutions to the TSP.

Genetic Algorithms

Another popular machine learning approach for solving TSP is genetic algorithms (GA). GA is a metaheuristic optimization algorithm inspired by the process of natural selection in genetics. In the context of TSP, a population of potential solutions (called chromosomes) is evolved over multiple generations. Each chromosome represents a possible route for the salesperson. Through processes like selection, crossover, and mutation, the genetic algorithm explores different combinations of cities to find better solutions. The fittest individuals from each generation are selected to produce the next generation, leading to the evolution of the population towards better solutions.

Overall, machine learning approaches offer promising solutions to the TSP and have the potential to outperform traditional optimization algorithms. As research in AI continues to evolve, we can expect further advancements in solving the traveling salesman problem and similar optimization problems using intelligent techniques.

Supervised Learning for TSP

The Traveling Salesman Problem (TSP) is a well-known optimization problem that involves finding the shortest possible route for a salesman to visit a given set of cities and return to the starting city. This problem has been extensively studied and has numerous applications in various industries.

One approach to solving the TSP is to use supervised learning techniques, which involve training a machine learning model to predict the optimal solution for a given set of cities. By using artificial intelligence (AI) and learning from existing solutions, the model can make predictions and find near-optimal solutions for new instances of the problem.

Training Data

To train the supervised learning model for TSP, a dataset consisting of input-output pairs is needed. Each input corresponds to a set of cities, represented by their coordinates, and the corresponding output is the optimal solution for that set of cities. The training data should cover a wide range of instances with different numbers of cities and complexities to ensure the model learns to generalize well.

Feature Engineering

Before training the model, feature engineering techniques can be applied to transform the raw input data into a format suitable for learning. This may involve calculating additional features such as distances between cities, angles between city coordinates, or any other relevant characteristics that can help the model learn patterns and make accurate predictions.

Training the Model

Various supervised learning algorithms can be used to train the model for TSP, such as decision trees, neural networks, or support vector machines. The choice of algorithm depends on factors such as dataset size, complexity, and desired performance.

The model is trained using the input-output pairs, and the objective is to minimize the prediction error by adjusting the model’s parameters or hyperparameters. Cross-validation techniques can be used to evaluate the model’s performance and prevent overfitting.

Once the model is trained, it can be used to predict the optimal solution for new sets of cities. The predicted solution may not always be the absolute optimal solution due to the complexity of the TSP, but supervised learning can provide good approximate solutions.

In conclusion, supervised learning techniques offer a promising approach to solving the Traveling Salesman Problem. By training a machine learning model using existing solutions, it can make predictions and provide near-optimal solutions for new instances of the problem. This application of artificial intelligence and learning has the potential to improve efficiency and decision-making in various industries that face similar optimization challenges.

Unsupervised Learning for TSP

The Traveling Salesman Problem (TSP) is a well-known problem in the field of artificial intelligence and machine learning. It involves finding the shortest possible route that a salesperson can take to visit a set of cities and return to the starting city. This problem is often used as a benchmark for testing optimization algorithms and techniques.

Traditionally, solving the TSP has been a challenging task, requiring the use of combinatorial optimization algorithms and heuristics. However, recent advancements in machine learning, particularly unsupervised learning techniques, have shown promise in tackling this problem.

Unsupervised learning is a branch of machine learning where the algorithm learns patterns and relationships within the data without any specific guidance or labeled examples. In the context of the TSP, unsupervised learning algorithms can be used to analyze the spatial relationships between the cities and learn optimal routes.

One approach is to use clustering algorithms to group cities that are close to each other. The algorithm can then find the optimal order to visit these clusters, reducing the complexity of the problem. Another approach is to use deep learning techniques, such as autoencoders, to learn a lower-dimensional representation of the cities and use this representation to find the shortest path.

By using unsupervised learning for the TSP, it is possible to find near-optimal solutions without explicitly defining the objective function or using heuristics. This reduces the computational complexity and can lead to more efficient and scalable solutions for large-scale TSP instances.

In conclusion, unsupervised learning techniques offer a new perspective on solving the Traveling Salesman Problem. By leveraging the power of artificial intelligence and machine learning, we can develop innovative approaches to solve this classic optimization problem efficiently and effectively.

Reinforcement Learning for TSP

Artificial Intelligence (AI) techniques have been widely applied to solve various real-world problems, and the Traveling Salesman Problem (TSP) is no exception. TSP is a classic optimization problem where a salesman needs to find the shortest possible route to visit a set of cities and return to the starting point.

In recent years, machine learning algorithms, particularly reinforcement learning, have shown promising results in tackling TSP. Reinforcement learning is a branch of AI that focuses on training agents to make sequential decisions based on environmental feedback. It has been successfully applied to various problems, including robotics, game playing, and now TSP.

In reinforcement learning for TSP, the salesman is treated as an agent that learns how to choose the next city to visit in order to minimize the total distance traveled. The agent receives rewards or penalties based on the choices it makes. By exploring different actions and learning from the feedback, the agent gradually improves its decision-making abilities.

One common approach to reinforcement learning for TSP is to use a policy-based method, where the agent learns a policy that maps states (current city and visited cities) to actions (next city to visit). The agent uses this learned policy to make decisions during the traversal of the cities. The policy is updated through a process called policy gradient, where the agent adjusts the probabilities assigned to each action based on the rewards received.

Another approach is to use value-based methods, where the agent learns the expected value (reward) of being in a certain state and taking a certain action. The agent then selects the action with the highest expected value at each step. This process is done iteratively, adjusting the value estimates based on the rewards received and the expected values of the next states.

Reinforcement learning for TSP is still an active area of research, and various techniques and algorithms are constantly being developed and improved. As AI techniques continue to advance, we can expect further progress in solving the traveling salesman problem and optimizing salesperson routes in the real world.

Hybrid AI Techniques for TSP

The Travelling Salesman Problem (TSP) is a classic optimization problem in artificial intelligence that involves finding the shortest possible route that a salesman can travel to visit a given set of cities and return to the starting point. Due to its computational complexity, solving the TSP is a challenging task.

To tackle the TSP, researchers have explored various artificial intelligence techniques. One approach is to combine multiple AI techniques to create hybrid algorithms that can yield better results. These hybrid AI techniques leverage the strengths of different AI algorithms to find efficient solutions for the TSP.

One popular hybrid AI technique for the TSP is the combination of machine learning and heuristic algorithms. Machine learning algorithms, such as genetic algorithms or neural networks, can be used to generate initial solutions for the TSP. These initial solutions can then be improved using heuristic algorithms, such as the 2-opt or 3-opt algorithm, which search for better solutions by iteratively swapping edges in the tour.

Another hybrid AI technique for the TSP is the combination of metaheuristic algorithms and local search algorithms. Metaheuristic algorithms, such as ant colony optimization or simulated annealing, can be used to explore the search space of the TSP and find promising solutions. These solutions can then be further refined using local search algorithms, which make small adjustments to the solutions to improve their quality.

Hybrid AI techniques offer the advantage of leveraging the complementary strengths of different AI algorithms to solve the TSP more effectively. By combining different techniques, hybrid algorithms can achieve better performance and find more optimal solutions compared to using a single AI technique alone.

In conclusion, solving the Travelling Salesman Problem (TSP) requires the use of advanced artificial intelligence techniques. Hybrid AI techniques that combine machine learning, heuristic algorithms, metaheuristic algorithms, and local search algorithms have shown great promise in solving the TSP efficiently. Further research and development in this area can lead to even more effective approaches for solving this challenging problem.

Combining Genetic Algorithms with Neural Networks for TSP

The Travelling Salesman Problem (TSP) is a classic optimization problem in which a salesperson must find the shortest possible route to visit a set of cities and return to the starting city. This problem has long captivated researchers in the field of Artificial Intelligence (AI) due to its complexity and real-world applications.

One common approach to solving the TSP is by using Genetic Algorithms (GA), which mimic the process of natural selection to find optimal solutions. GA starts with a population of candidate solutions, and through selection, reproduction, and mutation, it evolves towards finding a near-optimal solution.

Recently, researchers have started combining the power of Genetic Algorithms with Neural Networks (NN) to tackle the TSP. Neural Networks are machine learning models inspired by the structure and function of biological neural networks. They are adept at pattern recognition and can be trained to learn and make predictions based on training data.

In the context of the TSP, a Neural Network can be used to learn patterns and relationships in the problem space. The Neural Network is trained using genetic operators such as mutation and crossover, with the goal of finding a good initial solution for the TSP. The solution found by the Neural Network is then further improved using Genetic Algorithms.

This combination of Genetic Algorithms with Neural Networks leverages the strengths of both approaches. The Neural Network allows for efficient learning of patterns in the problem space, while the Genetic Algorithms provide global optimization capabilities and fine-tuning of the solution.

The use of Artificial Intelligence techniques, such as combining Genetic Algorithms with Neural Networks, has shown promising results in solving the TSP. This hybrid approach has the potential to find near-optimal solutions for the TSP, which can have significant practical applications in the field of logistics and operations research.

In conclusion, the combination of Genetic Algorithms and Neural Networks offers a powerful approach to tackle the Travelling Salesman Problem. This hybrid AI technique can efficiently learn from data and optimize the solution, providing a valuable tool for solving complex optimization problems like the TSP.

Combining Ant Colony Optimization with Reinforcement Learning for TSP

The Travelling Salesperson Problem (TSP) is a classic problem in the field of artificial intelligence (AI) and is often used as a benchmark for testing various optimization algorithms. The goal of the TSP is to find the shortest possible route that a salesperson can take to visit a set of cities and return to the starting city, while visiting each city exactly once.

Ant Colony Optimization (ACO) is a metaheuristic algorithm inspired by the behavior of ants searching for food. The idea behind ACO is to simulate the pheromone trail left by ants to guide their search. By iteratively updating the pheromone trail based on the quality of the solutions found, ACO is able to converge to a near-optimal solution to the TSP.

Reinforcement Learning (RL) is a machine learning technique that focuses on how an agent can learn from interactions with a dynamic environment. In the context of the TSP, RL can be used to train an agent to navigate the cities efficiently. The agent receives a reward signal based on the quality of the solution found, and it uses this feedback to update its policy for selecting which city to visit next.

Combining ACO with RL

One approach to solving the TSP is to combine ACO with RL. In this approach, an ant colony is used to explore the solution space and update the pheromone trail, while a reinforcement learning agent learns from the ants’ behavior to improve its policy for selecting the next city to visit.

The ant colony proceeds by iteratively constructing solutions to the TSP. Each ant starts at a random city and selects the next city to visit based on the pheromone trail and a heuristic value that estimates the desirability of visiting each city. After completing a solution, the pheromone trail is updated based on the quality of the solution found.

The reinforcement learning agent observes the ants’ behavior and receives a reward signal based on the quality of the solution found. It then updates its policy for selecting the next city to visit using techniques such as Q-learning or policy gradients. The updated policy is used by the ant colony in the next iteration to guide its search.

Benefits and Challenges

The combination of ACO with RL offers several benefits in solving the TSP. Firstly, it leverages the exploration-exploitation trade-off of ACO to explore the solution space effectively. The RL agent, on the other hand, learns from the ants’ behavior and can adapt its policy to the specific characteristics of the problem instance.

However, combining ACO with RL also poses challenges. Balancing the exploration and exploitation in the ant colony is crucial to prevent premature convergence to suboptimal solutions. The RL agent needs to explore different strategies effectively and continuously learn and update its policy based on the reward signal.

The combination of Ant Colony Optimization with Reinforcement Learning is a promising approach to solving the Travelling Salesperson Problem. By leveraging the strengths of both techniques, it is possible to achieve near-optimal solutions to this challenging problem. Further research and experimentation are needed to explore the full potential of this hybrid approach and its application to other optimization problems in the field of artificial intelligence.

Combining Simulated Annealing with Tabu Search for TSP

The Travelling Salesman Problem (TSP) is a well-known problem in the field of Artificial Intelligence (AI) and Machine Learning. It involves finding the shortest possible route for a salesman to visit a number of cities and return to the starting point.

TSP is known to be an NP-hard problem, meaning that finding the optimal solution requires an exponential amount of time as the number of cities increases. Various AI techniques have been developed to solve TSP efficiently, and two popular ones are Simulated Annealing and Tabu Search.

Simulated Annealing is a metaheuristic algorithm inspired by the annealing process in metallurgy. It starts with an initial solution and iteratively explores neighboring solutions by making random changes. The algorithm gradually decreases the probability of accepting worse solutions, allowing it to escape local optima and converge towards a global optimum.

Tabu Search, on the other hand, is a local search algorithm that maintains a short-term memory of previously visited solutions. It forbids revisiting those solutions for a certain number of iterations, preventing the algorithm from getting stuck in cycles or revisiting suboptimal solutions.

Combining Simulated Annealing with Tabu Search for TSP can lead to improved performance and better results. The simulated annealing algorithm can be used to generate initial solutions, while the tabu search algorithm can be used to further explore and refine those solutions. This combination allows for a more effective exploration of the search space and a better chance of finding the optimal solution.

In summary, combining simulated annealing with tabu search is a promising approach for solving the TSP. It combines the global exploration capability of simulated annealing with the local search and memory-based strategies of tabu search. By leveraging the strengths of both algorithms, this approach can help find high-quality solutions to the travelling salesman problem efficiently and effectively.

Comparison of AI Techniques for Solving TSP

The Travelling Salesman Problem (TSP) is a well-known problem in the field of artificial intelligence and machine learning. The TSP involves finding the shortest possible route that a salesman can take to visit a given set of cities exactly once and return to the starting city. It is a classic problem that has been studied extensively in the field of computer science.

There are several AI techniques that have been used to tackle the TSP, each with its own advantages and disadvantages. One popular approach is to use genetic algorithms, which are inspired by the process of natural selection. In this approach, a population of potential solutions is evolved over multiple generations, with the fittest individuals being selected to produce offspring. This process continues until a satisfactory solution is found.

Another popular technique for solving the TSP is the use of ant colony optimization algorithms. These algorithms are inspired by the behavior of ants, who use pheromone trails to communicate and navigate their environment. In this approach, artificial ants are used to explore the solution space, leaving pheromone trails that are reinforced based on the quality of the solutions found. Over time, a good solution is discovered based on the concentration of pheromones.

Machine learning techniques have also been applied to the TSP, with some success. In these approaches, a model is trained on a set of known TSP instances, and then used to predict the optimal solution for new instances. This can be done using techniques such as reinforcement learning or supervised learning.

Overall, each AI technique has its own strengths and weaknesses when applied to the TSP. Genetic algorithms are powerful and can find good solutions, but they can be computationally expensive. Ant colony optimization algorithms are efficient and can find near-optimal solutions, but they may struggle with larger instances of the problem. Machine learning techniques have the potential to generalize well, but they may require a large amount of training data.

In conclusion, there are various AI techniques that can be used to tackle the Travelling Salesman Problem. Each technique has its own pros and cons, and the choice of technique will depend on the specific requirements of the problem at hand. It is important to consider factors such as computational efficiency, solution quality, and the availability of training data when choosing an AI technique for solving the TSP.

Pros and Cons of AI Techniques for TSP

Artificial Intelligence (AI) techniques have shown great promise in solving the Travelling Salesman Problem (TSP). The TSP is a classic combinatorial optimization problem, where a salesperson must find the shortest possible route to visit a set of cities exactly once and return to the starting city.

Pros of Using AI Techniques for TSP

1. Improved Efficiency: AI techniques, such as machine learning, can significantly improve the efficiency of finding optimal or near-optimal solutions for TSP. These techniques can explore a large search space efficiently and provide solutions that are better than those obtained from traditional methods.

2. Global Optimization: AI techniques can help in finding global optimal solutions for TSP. Traditional optimization methods may find local optima, which are not the best possible solutions. With AI techniques, the entire search space can be explored, leading to better solutions.

3. Adaptability: AI techniques can adapt to different instances of the TSP. This means that they can learn from previous instances and apply the knowledge gained to solve new instances more efficiently. This adaptability makes AI techniques suitable for solving TSP in real-world scenarios.

Cons of Using AI Techniques for TSP

1. Computational Complexity: AI techniques for solving TSP can be computationally expensive, especially when dealing with a large number of cities. The time complexity of these techniques may hinder their practicality in real-time decision-making scenarios.

2. Problem Dependency: AI techniques for solving TSP may heavily depend on the problem instance. Different instances of the TSP may require different AI techniques or parameter tuning, which can be time-consuming and computationally expensive.

3. Interpretability: AI techniques, such as machine learning based approaches, may lack interpretability. The solutions provided by these techniques may be difficult to explain or understand, especially when compared to traditional optimization methods.

Overall, AI techniques have the potential to provide efficient solutions for the Travelling Salesman Problem. While there are challenges to overcome, such as computational complexity and interpretability, the benefits of using AI techniques outweigh the drawbacks in many cases.

Real-World Applications of AI Techniques for TSP

The Travelling Salesman Problem (TSP) is a well-known problem in artificial intelligence and machine learning. It involves finding the shortest possible route that a salesperson can take to visit a given set of cities exactly once and return to the starting city. The TSP has been extensively studied and has numerous real-world applications.

Logistics and Supply Chain Management

One of the main applications of AI techniques for TSP is in logistics and supply chain management. Companies that have multiple warehouses or distribution centers need to optimize the routes their delivery vehicles take to minimize costs and maximize efficiency. AI algorithms can be used to solve the TSP for these companies, providing them with the most optimal routes for their delivery vehicles.

Circuit Board Design

Another real-world application of AI techniques for TSP is in circuit board design. When designing a circuit board, engineers need to determine the most efficient way to connect various components on the board. This can be formulated as a TSP, with the components representing cities and the connections representing distances between them. AI algorithms can be used to solve this TSP and find the most optimal connections between the components.

These are just a few examples of the real-world applications of AI techniques for TSP. There are many other areas where TSP can be applied, such as route planning for autonomous vehicles, network routing optimization, and DNA sequencing. AI techniques are invaluable tools for solving the TSP and finding optimal solutions for a wide range of problems.

Challenges in Solving TSP with AI Techniques

The Travelling Salesman Problem (TSP) is a classic optimization problem that deals with finding the shortest possible route for a salesman to travel and visit a set of cities exactly once and return to the starting city. Solving TSP is a complex task and requires the use of AI techniques such as machine learning and artificial intelligence (AI).

One of the major challenges in solving TSP with AI techniques is the exponential growth of the problem as the number of cities increases. The number of possible routes to visit all cities grows factorially with the number of cities, making it computationally expensive to find the optimal solution.

Another challenge is the high dimensionality of the problem. TSP can be represented as a graph with cities as nodes and the distances between cities as edges. The number of edges in the graph is equal to the number of possible connections between cities, which grows quadratically with the number of cities. This high dimensionality makes it difficult to explore all possible solutions and find the optimal one.

Furthermore, TSP is an NP-hard problem, which means that it is difficult to find an exact solution in a reasonable amount of time. AI techniques provide approximate solutions that are close to the optimal solution, but these solutions may not be guaranteed to be optimal. Finding good quality solutions with AI techniques is a challenge in itself.

Moreover, the performance of AI techniques in solving TSP heavily depends on the choice of algorithms and parameters. Different AI techniques such as genetic algorithms, ant colony optimization, and reinforcement learning have been applied to TSP, but their effectiveness varies depending on the problem instance and the specific parameters used. Finding the right combination of techniques and parameters is a challenging task.

In conclusion, solving TSP with AI techniques poses several challenges such as the exponential growth and high dimensionality of the problem, the NP-hardness, and the need for selecting appropriate algorithms and parameters. Addressing these challenges is crucial for obtaining efficient and accurate solutions to the TSP.

Future Trends in AI Techniques for TSP

As the world becomes more interconnected and the need for efficient transportation grows, finding optimal solutions to the Travelling Salesperson Problem (TSP) becomes increasingly important. Artificial intelligence (AI) techniques have shown great promise in tackling this complex problem, and the future holds even more potential.

One of the most exciting trends in AI techniques for TSP is the incorporation of machine learning algorithms. By analyzing large amounts of data, these algorithms can identify patterns and make predictions about the most efficient routes for a travelling salesperson. This can greatly reduce the search space and lead to faster and more accurate solutions.

Another trend is the development of hybrid AI techniques that combine the strengths of different algorithms. For example, a combination of genetic algorithms and simulated annealing can provide a more comprehensive search strategy, improving the chances of finding the optimal solution to the TSP. These hybrid techniques have shown promising results and are expected to be further refined in the future.

In addition to machine learning and hybrid techniques, advancements in AI hardware, such as faster processors and more memory, are also expected to have a significant impact on solving the TSP. With more computing power, AI algorithms can handle larger problem instances and provide more accurate solutions. This opens up new possibilities for solving real-world TSP scenarios, where the number of cities and constraints can be very high.

Furthermore, the integration of AI techniques with other emerging technologies, such as blockchain and Internet of Things (IoT), can bring a new dimension to solving the TSP. For example, by leveraging IoT data from vehicles and traffic sensors, AI algorithms can dynamically adjust the salesperson’s route based on real-time traffic conditions, leading to more efficient and adaptive solutions.

In conclusion, the future of solving the Travelling Salesperson Problem with AI techniques looks bright. With advancements in machine learning, hybrid algorithms, hardware capabilities, and the integration of AI with other technologies, we can expect more efficient and accurate solutions for the TSP. This will not only benefit businesses and salespersons, but also contribute to the overall optimization of transportation systems.

Question-answer:

What is the traveling salesperson problem.

The Traveling Salesperson Problem, also known as TSP, is a classic algorithmic problem in computer science. It involves finding the shortest possible route that a salesperson can take to visit a set of cities and return to the starting city, while visiting each city exactly once.

Why is the Traveling Salesperson Problem important?

The Traveling Salesperson Problem is important because it has practical applications in various fields, such as logistics, transportation, and network routing. Solving this problem efficiently can lead to cost savings and improved efficiency.

How can Artificial Intelligence techniques be used to solve the Traveling Salesperson Problem?

Artificial Intelligence techniques, such as genetic algorithms, ant colony optimization, and simulated annealing, can be used to solve the Traveling Salesperson Problem. These algorithms mimic natural processes to search for optimal or near-optimal solutions.

What is the role of machine learning in solving the Traveling Salesperson Problem?

Machine learning can be used in various ways to solve the Traveling Salesperson Problem. For example, reinforcement learning algorithms can learn to find good solutions through trial and error, while supervised learning can be used to train models that predict the optimal route given a set of cities.

What are the limitations of using Artificial Intelligence techniques to solve the Traveling Salesperson Problem?

While Artificial Intelligence techniques can provide good solutions to the Traveling Salesperson Problem, they are not guaranteed to find the optimal solution. These algorithms can also be computationally expensive and may require significant computational resources to solve large-scale instances of the problem.

What is the Traveling Salesman Problem?

The Traveling Salesman Problem (TSP) is a classic combinatorial optimization problem in mathematics and computer science. It involves finding the shortest possible route that allows a salesman to visit a set of cities and return to the original city, visiting each city only once. The problem is known to be NP-hard, meaning that finding an exact solution becomes extremely time-consuming as the number of cities increases.

How can Artificial Intelligence techniques be used to solve the Traveling Salesman Problem?

Artificial Intelligence techniques, such as optimization algorithms and machine learning, can be applied to solve the Traveling Salesman Problem. Optimization algorithms like genetic algorithms, ant colony optimization, and simulated annealing can be used to find approximate solutions that are close to the optimal route. Machine learning techniques can also be used to learn patterns and heuristics from previous solutions, which can help improve the efficiency of finding good solutions.

What are the challenges in solving the Traveling Salesman Problem using AI techniques?

One of the main challenges in using AI techniques to solve the Traveling Salesman Problem is the exponential increase in the search space as the number of cities increases. This makes finding an exact solution computationally expensive and impractical for large problem instances. Additionally, finding good solutions that are close to the optimal route is still a challenging task, as it requires balancing exploration and exploitation in the search process. Finally, determining the stopping criteria for the algorithms and evaluating the quality of the solutions obtained are also challenging aspects of solving TSP using AI techniques.

About the author

Cohere: Bridging Language and AI for a Smarter Future

Microsoft office 365 ai. microsoft copilot, understanding the distinctions between artificial intelligence and human intelligence, exploring the impact of artificial intelligence on discrimination in insurance pricing and underwriting.

COMMENTS

Travelling salesman problem
In these applications, the concept city represents, for example, customers, soldering points, ... In March 2005, the travelling salesman problem of visiting all 33,810 points in a circuit board was solved using Concorde TSP Solver: a tour of length 66,048,945 units was found, and it was proven that no shorter tour exists. The computation took ...
Traveling Salesman Problem (TSP) Implementation
Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once.
Traveling Salesperson Problem
The traveling salesperson problem can be modeled as a graph. Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path ...
Traveling salesman problem
The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, ... In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community.
PDF The Traveling Salesman Problem
The traveling salesman problem is solved if there exists a shortest route that visits each destination once and permits the salesman to return home. (This route is called a Hamiltonian Cycle and will be explained in Chapter 2.) The traveling salesman problem can be divided into two types: the problems where there is a path between ...
What is the Travelling Salesperson Problem (TSP)?
The Travelling Salesperson Problem (TSP), or sometimes known as the Travelling Salesman Problem, is the challenge of determining the quickest path for your delivery drivers, field sales representatives, and service reps given a list of specific locations. Let's look at an example to better grasp the issue: A salesman wants to sell his ...
Traveling salesman problem
traveling salesman problem, an optimization problem in graph theory in which the nodes (cities) of a graph are connected by directed edges (routes), where the weight of an edge indicates the distance between two cities. The problem is to find a path that visits each city once, returns to the starting city, and minimizes the distance traveled. ...
Explained: What is Traveling Salesman Problem (TSP)
The traveling Salesman Problem (TSP) is a combinatorial problem that deals with finding the shortest and most efficient route to follow for reaching a list of specific destinations. It is a common algorithmic problem in the field of delivery operations that might hamper the multiple delivery process and result in financial loss. TSP turns out ...
12.9 Traveling Salesperson Problem
The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method. The steps in the brute force method are: Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights. Step 2: List all possible Hamilton cycles.
Traveling Salesman Problem
2.1 Defining the TSP. A problem is the frame into which the solutions fall. The design of a search system to solve an optimization problem and study of the related search behavior are based on how the problem is defined. The assumptions about the properties of the problem must be explicated into the problem definition.
Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is perhaps the most studied discrete optimization problem. Its popularity is due to the facts that TSP is easy to formulate, difficult to solve, and has a large number of applications. It appears that K. Menger was the first researcher to consider the Traveling Salesman Problem (TSP). He observed that the ...
Traveling salesman problem: a perspective review of recent research and
The traveling salesman problem (TSP) is one of the most studied problems in computational intelligence and operations research. Since its first formulation, a myriad of works has been published proposing different alternatives for its solution. ... In Section 9.4, the concepts behind NS are introduced, placing emphasis on how we have hybridized ...
Modeling the Traveling Salesman Problem from first principles
Figure 2.2. Minimalist workflow to problem-solving in OR. 2nd stage: conceptual model (Image by author) The purpose of the conceptual model is to state the problem using words, but in a standardized format, so that the mapping between "sentences" and "mathematical objects" becomes clear later in the subsequent phase (mathematical model formulation).
traveling salesman problem (TSP)
The traveling salesman problem (TSP) is an algorithmic problem tasked with finding the shortest route between a set of points and locations that must be visited. In the problem statement, the points are the cities a salesperson might visit. The salesman's goal is to keep both the travel costs and the distance traveled as low as possible.
PDF The Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is one of the most well-known combinatorial ... Instead, we describe the concepts informally based on intuition and some experimental results. The study of new search algorithms for the TSP continues to be a vibrant, excit- ing and fruitful endeavor in combinatorial optimization, computational mathematics ...
Travelling Salesman Problem
The Travelling Salesman Problem (also known as the Travelling Salesperson Problem or TSP) is an NP-hard graph computational problem where the salesman must visit all cities (denoted using vertices in a graph) given in a set just once. The distances (denoted using edges in the graph) between all these cities are known.
12.10: Traveling Salesperson Problem
The Brute Force Method. The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method. The steps in the brute force method are: Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.
Travelling Salesman Problem (Greedy Approach)
Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G') which will record the path the salesman is going to take from one node to another. The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance. The first edge selected is the ...
What is a Traveling Salesman Problem? Explained and Solved
Here are the Top 5 solutions to the Traveling Salesman Problem (TSP): 1. Brute Force Algorithm. The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all.
The Travelling Salesman Problem (TSP)
The travelling salesman problem (TSP) refers to the efforts of a door-to-door salesman trying to find the shortest and/or quickest way to serve all of the stops on his list of visits in a given time period (usually a working day).. Although it was once the problem of a salesperson, today there are far more workers that are faced with it. In recent years, the explosion of eCommerce and online ...
A concise guide to the Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is arguably the most famous problem in combinatorial optimization.Simply stated, it consists of determining a shortest tour passing exactly once through each of the n vertices of a graph (such a tour is called Hamiltonian).In its most common interpretation, the TSP is the problem of constructing a shortest salesman tour through n cities.
The Traveling Salesperson Problem
The "traveling salesperson" problem is a classic route selection problem where a sequence of locations has to be traveled to, and a return must be made to the starting location. Each location can only be traveled once. In the above example, a salesperson, starting at point 1, must visit six locations (1 to 6) and return to the starting point.
Travelling Salesman Problem: Solving with Artificial Intelligence
The Travelling Salesman Problem (TSP) is a classic optimization problem in artificial intelligence that involves finding the shortest possible route that a salesman can travel to visit a given set of cities and return to the starting point. Due to its computational complexity, solving the TSP is a challenging task.

BFS and DFS on Graph

Cycle in a Graph

Shortest Paths in Graph

Minimum Spanning Tree in Graph

Topological Sorting in Graph

Connectivity of Graph

Maximum flow in a Graph

Some must do problems on Graph

Traveling Salesman Problem (TSP) Implementation

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Traveling Salesperson Problem

Relationship to Graphs

Traveling salesman problem

Description

Classifications of the TSP

Variations of the TSP

Formulation

aTSP ILP Formulation

sTSP ILP Formulation

Exact algorithms

Heuristic algorithms

Tour construction procedures

Tour improvement procedures

Applications

Navigation menu

What is the Travelling Salesperson Problem (TSP)?

What is the quickest route for the salesman to take to visit each place only once before returning to the starting point?

Table of Contents

About Roundtrip

Check out these other articles

Use Delivery Management Software to Deliver Profits

How to Select the Right Route Planner for Your Deliveries

Drive Success: Optimize Routes, Reduce Costs

Designed to make deliveries easy

Explained: What is Traveling Salesman Problem (TSP)

What are Some Popular Solutions to Traveling Salesman Problem?

What is Traveling Salesman Problem (TSP)?

How difficult is it to solve?

Common Challenges of Traveling Salesman Problem (TSP)

1. Nearest Neighbor (NN)

2. The Branch and Bound Algorithm

3. The Brute Force Algorithm

How TSP and VRP Combinedly Pile Up Challenges?

Is there any real world solution to TSP and VRP?

Can a Route Planner Resolve the Traveling Salesman Problem (TSP)?

Create Optimized Routes Using Upper and Bid Goodbye to Traveling Salesman Problem

12.9 Traveling Salesperson Problem

Brute Force and Greedy Algorithms

Example 12.42

Your Turn 12.42

Finding Weights of All Hamilton Cycles in Complete Graphs

Example 12.43

Your Turn 12.43

Example 12.44

Your Turn 12.44

The Nearest Neighbor Method

Example 12.45

Your Turn 12.45

DAA Tutorial

Help Others, Please Share

Learn Latest Tutorials

Preparation

Trending Technologies

B.Tech / MCA

12.10: Traveling Salesperson Problem

Learning Objectives

Brute Force and Greedy Algorithms

Example 12.42

Your Turn 12.42

Finding Weights of All Hamilton Cycles in Complete Graphs

Example 12.43

Your Turn 12.43

Example 12.44

Your Turn 12.44

The Nearest Neighbor Method

Example 12.45

Your Turn 12.45

Travelling Salesman Problem (Greedy Approach)