travel time equation

The Enlightened Mindset

Exploring the World of Knowledge and Understanding

Welcome to the world's first fully AI generated website!

How to Calculate Travel Time Formula: A Step-by-Step Guide

By Happy Sharer

Introduction

The travel time formula is used to calculate the amount of time it takes to travel from one location to another. This formula is often used by travelers, transportation companies, and logistics professionals when planning trips or routes. This article will provide an overview of the travel time formula, explain how to calculate travel time, and examine the factors that can affect the calculation.

Explaining the Travel Time Formula Step-by-Step

To calculate travel time, you must first determine the distance, speed, and time for the route. Distance is simply the total length of the journey, while speed is the average speed at which the journey will be completed. Finally, time is the total amount of time it will take to complete the journey. Once these three variables have been determined, you can use the following equation to calculate travel time:

Travel Time = Distance / Speed

For example, if you are travelling 100 miles at a speed of 50 miles per hour, the travel time would be calculated as follows:

Travel Time = 100 miles / 50 miles per hour = 2 hours

Using Examples to Illustrate How to Calculate Travel Time

To further illustrate how to calculate travel time, let’s look at two examples. In the first example, a person is travelling from Los Angeles to San Francisco, a distance of about 400 miles. The person plans to drive at an average speed of 70 miles per hour. To calculate the travel time, we plug the values into the equation:

Travel Time = 400 miles / 70 miles per hour = 5.71 hours

In the second example, a person is travelling from London to Paris, a distance of about 350 miles. The person plans to fly at an average speed of 500 miles per hour. To calculate the travel time, we plug the values into the equation:

Travel Time = 350 miles / 500 miles per hour = 0.7 hours (or 42 minutes)

Breaking Down the Components of the Travel Time Formula

Now that we’ve seen how to calculate travel time with the formula, let’s take a closer look at each component of the equation.

Distance is the total length of the journey in miles or kilometers. It’s important to note that some routes may be longer than others due to detours or traffic. Therefore, it’s best to estimate the distance before calculating travel time.

Speed is the average speed at which the journey will be completed, usually measured in miles or kilometers per hour. It’s important to consider the speed limits on the roads or airways you’ll be travelling on, as well as any potential delays such as traffic or weather.

Time is the total amount of time it will take to complete the journey. This can be measured in hours, minutes, or seconds depending on the level of precision you need.

Comparing Different Travel Time Formulas

The travel time formula can be used to calculate the time it takes to travel by car, plane, or even on foot. Each mode of transportation has its own unique formula for calculating travel time.

Driving Time

When travelling by car, the travel time formula is typically used. This formula takes into account the distance, speed, and time needed to complete the journey.

Flying Time

When travelling by plane, the flight time formula is often used. This formula takes into account the distance between two airports, the average speed of the aircraft, and the total time needed to complete the journey.

Walking Time

When travelling by foot, the walking time formula is often used. This formula takes into account the distance, average walking speed, and total time needed to complete the journey.

Examining Variables That Affect Travel Time

In addition to the variables used in the travel time formula, there are also other external factors that can affect the calculation. For example, weather conditions and traffic congestion can both impact the amount of time it takes to complete a journey.

Weather Conditions

Weather conditions can have a significant impact on travel time. For example, inclement weather such as rain or snow can slow down a vehicle’s speed, resulting in increased travel time.

Traffic Congestion

Traffic congestion can also affect travel time. During peak hours, roads may be more congested, resulting in slower speeds and increased travel time.

Creating a Travel Time Calculator Tool

A travel time calculator is a useful tool for travelers, transportation companies, and logistics professionals. This tool can be used to quickly calculate travel time based on distance, speed, and time. Here are some benefits of using a travel time calculator:

• Save time: Calculating travel time manually can be time-consuming. With a travel time calculator, you can quickly and accurately calculate travel time.
• Reduce errors: Manually calculating travel time can lead to errors. With a travel time calculator, you can reduce the risk of making mistakes.
• Increase efficiency: A travel time calculator can help you plan your trips more efficiently.

If you’re interested in creating a travel time calculator, here are some guidelines to follow:

• Determine the type of calculator you want to create. Do you want to create a calculator for cars, planes, or walking?
• Gather the necessary data. You will need to collect data on distances, speeds, and times for the calculator.
• Design the user interface. This should be easy to use and understand.
• Test the calculator. Test the calculator to ensure it works correctly.
• Launch the calculator. Once the calculator is tested, you can launch it for public use.

The travel time formula is a useful tool for calculating the amount of time it takes to travel from one location to another. By understanding the components of the formula and the factors that can affect the calculation, you can calculate travel time more accurately. Additionally, you can create a travel time calculator tool to save time and increase efficiency.

(Note: Is this article not meeting your expectations? Do you have knowledge or insights to share? Unlock new opportunities and expand your reach by joining our authors team. Click Registration to join us and share your expertise with our readers.)

Hi, I'm Happy Sharer and I love sharing interesting and useful knowledge with others. I have a passion for learning and enjoy explaining complex concepts in a simple way.

Related Post

Exploring japan: a comprehensive guide for your memorable journey, your ultimate guide to packing for a perfect trip to hawaii, the ultimate packing checklist: essentials for a week-long work trip, leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Expert Guide: Removing Gel Nail Polish at Home Safely

Trading crypto in bull and bear markets: a comprehensive examination of the differences, making croatia travel arrangements, make their day extra special: celebrate with a customized cake.

• Skip to main content
• Skip to primary sidebar

Distance and Average Speed to Travel Time Calculator

Click save settings to reload page with unique web page address for bookmarking and sharing the current tool settings

✕ clear settings

Flip tool with current settings and calculate average speed or total distance

Related Tools

• Average speed calculator
• Travel distance calculator
• Convert speed into different units
• Convert distance into different units
• Convert time duration into different units

This calculator will estimate the travel time for a journey using the travel distance to destination and the expected average speed of the method of travel.

Once a distance and speed have been entered the calculated time will be displayed in the answer box. Also a conversion scale will be generated for different values of distance versus time at the same speed.

This tool estimates the journey time with the following formula:

• d = Distance

Distance Travelled

Enter the expected distance to be travelled in any units.

Average Speed

Enter the estimated average speed of the intended method of transport.

Time Estimate

This is an estimate of the total time it will take to complete the journey without any delays.

Module 9: Multi-Step Linear Equations

Using the distance, rate, and time formula, learning outcomes.

• Use the problem-solving method to solve problems using the distance, rate, and time formula

One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you traveled if you drove at a steady rate of [latex]60[/latex] miles per hour for [latex]2[/latex] hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said [latex]120[/latex] miles, you already know how to use this formula!

The math to calculate the distance might look like this:

[latex]\begin{array}{}\\ \text{distance}=\left(\Large\frac{60\text{ miles}}{1\text{ hour}}\normalsize\right)\left(2\text{ hours}\right)\hfill \\ \text{distance}=120\text{ miles}\hfill \end{array}[/latex]

In general, the formula relating distance, rate, and time is

[latex]\text{distance}\text{=}\text{rate}\cdot \text{time}[/latex]

Distance, Rate, and Time

For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula

[latex]d=rt[/latex]

where [latex]d=[/latex] distance, [latex]r=[/latex] rate, and [latex]t=[/latex] time.

Notice that the units we used above for the rate were miles per hour, which we can write as a ratio [latex]\Large\frac{miles}{hour}[/latex]. Then when we multiplied by the time, in hours, the common units “hour” divided out. The answer was in miles.

Jamal rides his bike at a uniform rate of [latex]12[/latex] miles per hour for [latex]3\Large\frac{1}{2}[/latex] hours. How much distance has he traveled?

In the following video we provide another example of how to solve for distance given rate and time.

Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of [latex]520[/latex] miles. If he can drive at a steady rate of [latex]65[/latex] miles per hour, how many hours will the trip take?

Show Solution

In the following video we show another example of how to find rate given distance and time.

• Question ID 145550, 145553,145619,145620. Authored by : Lumen Learning. License : CC BY: Attribution
• Ex: Find the Rate Given Distance and Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/3rYh32ErDaE . License : CC BY: Attribution
• Example: Solve a Problem using Distance = Rate x Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/lMO1L_CvH4Y . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Speed, Distance & Time Calculator

Use this speed calculator to easily calculate the average speed, distance travelled and the trip duration of a vehicle: car, bus, train, bike, motorcycle, plane etc. Works with miles, feet, kilometers, meters, etc..

Related calculators

• Speed, Distance & Time Calculation
• Average Speed formula
• Distance formula
• Duration (Time) formula
• How to calculate the average speed of a car?

    Speed, Distance & Time Calculation

In order to use the above speed, distance & time calculator, or do such math on your own, you will need to know two out of three metrics: speed, distance, time. You will need to convert the metrics to the same time and distance units, e.g. miles, kilometers, meters, yards, feet, and hours, minutes or seconds. For example, if you have speed in mph (miles per hour), time should also be in hours. If you have distance in kilometers, then speed should also be in km/h (kilometers per hour).

The unit of the result will depend on the units you input, but our speed calculator will conveniently display additional units where appropriate.

    Average Speed formula

The formula for average speed, also called average velocity in physics and engineering, is:

where v is the velocity, d is the distance, and t is the time, so you can read it as Speed = Distance / Time . As noted above, make sure you convert the units appropriately first, or use our speed calculator which does that automatically. The resulting unit will depend on the units for both time and distance, so if your input was in miles and hours, the speed will be in mph. If it was in meters and seconds, it will be in m/s (meters per second).

Example: If you took a plane from New York to Los Angeles and the flight was 5 hours of air time, what was the speed of the plane, given that the flight path was 2450 miles? The answer is 2450 / 5 = 490 mph (miles per hour) average speed. If you want the result in km/h, you can convert from miles to km to get 788.58 km/h.

    Distance formula

The formula for distance, if you know time (duration) and the average speed, is:

Example: If a truck travelled at an average speed of 80 km per hour for 4 hours, how many miles did it cover in that time? To find the miles covered, first, calculate 80 * 4 = 320 km, then convert km to miles by dividing by 1.6093 or by using our km to miles converter to get the answer: 198.84 miles.

    Duration (Time) formula

The time, or more precisely, the duration of the trip, can be calculated knowing the distance and the average speed using the formula:

where d is the distance travelled, v is the speed (velocity) and t is the time, so you can read it as Time = Distance / Speed . Make sure you convert the units so both their distance and time components match, or use our trip duration calculator above which will handle conversions automatically. For example, if you have distance in miles and speed in km/h, you will need to convert speed to mph or distance to kilometers. The time unit of the result will match the time unit of the speed measure, so if it is measured in something per hour, the result will be in hours. If it is measured in some unit per second, the result will be in seconds.

Example: If a train can travel 500 miles with an average speed of 50 miles per hour, how long it would take it to complete a 500-mile route? To find the answer, use the formula and substitute the values, resulting in 500 / 50 = 10 hours.

    How to calculate the average speed of a car?

Say you travelled a certain distance with a car or another vehicle and you want to calculate what its average speed was. The easiest way to do that would be by using the calculator above, but if you prefer, you can also do the math yourself. Either way, you need to know the distance to a satisfactory approximation, for which you can use a map (e.g. Google Maps) to measure the distance from point to point. Make sure you measure closely to the path you took, and not via a straight line, unless you travelled by air in which case that would be a good approximation. Of course, having a GPS reading of the distance would be more precise. Then you need to know the travel time. Make sure you subtract any rests or stops you made from the total trip duration.

If the total distance travelled was 500 miles and the time it took you was 5 hours, then your average speed was 500 / 5 = 100 miles per hour (mph). If the distance was 300 kilometers and it took you 5 hours to cover it, your speed was 300 / 5 = 60 km/h (kilometers per hour).

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Speed Distance Time Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/speed-calculator.php URL [Accessed Date: 21 Apr, 2024].

     Transportation calculators

Get 25% off all test packages.

Get 25% off all test packages!

Click below to get 25% off all test packages.

How to Calculate Speed, Distance & Time

Working out speed, distance and time is an important part of many roles, including those in the armed forces or transport industries.

If you are applying for a role in these industries, you may be tested on this as part of your recruitment process. The questions will allow your employer to test your applied mathematical abilities.

How to calculate speed, distance & time: the formula triangle you’ll need?

To work out speed, divide the distance of the journey by the time it took to travel, so speed = distance divided by time. To calculate time, divide the distance by speed. To get the distance, multiply the speed by time.

You may see these equations simplified as s=d/t, where s is speed, d is distance, and t is time.

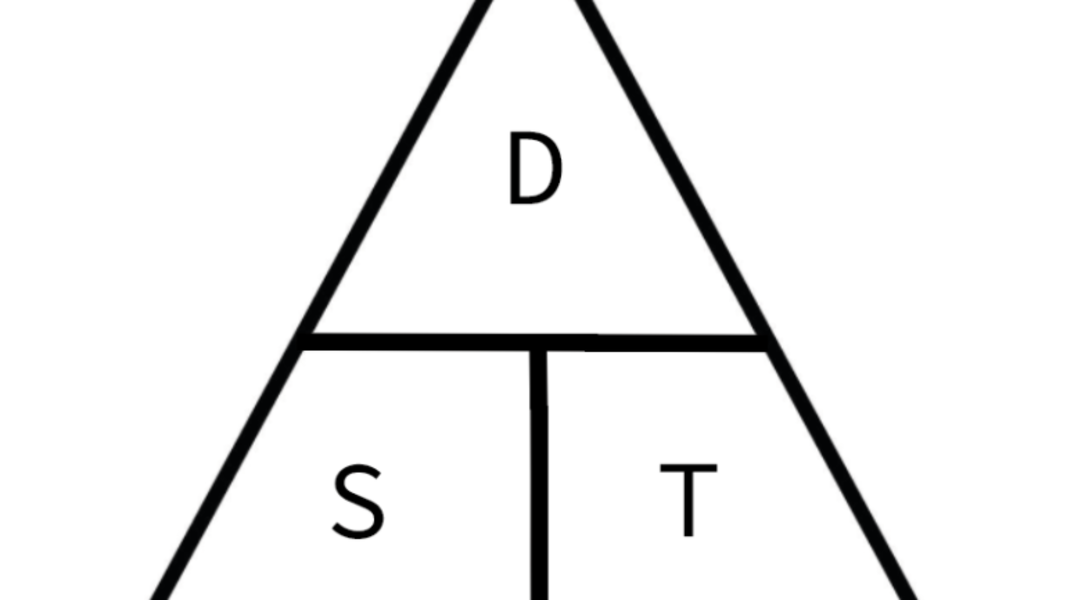
This formula can be arranged into the triangle above. In the triangle, speed and time form the base, as they are what is multiplied together to work out the distance.

The triangle is an easy way to remember the formula and can save you time when working out your exam questions. The triangle will help you remember the three formulas:

• The formula of speed is Speed = Distance ÷ Time
• The formula of time is Time = Distance ÷ Speed
• The formula of distance is Distance = Speed x Time

The triangle shows you what calculation you should use. As distance is at the top of the triangle, to work it out, you need to multiply speed with time.

As speed and time are at the bottom of the triangle, you need to divide this number from the figure for distance, to work out the correct answer.

When beginning to study for your practice test, make sure you write out the triangle on your paper. This will help you to memorize it.

How to calculate speed

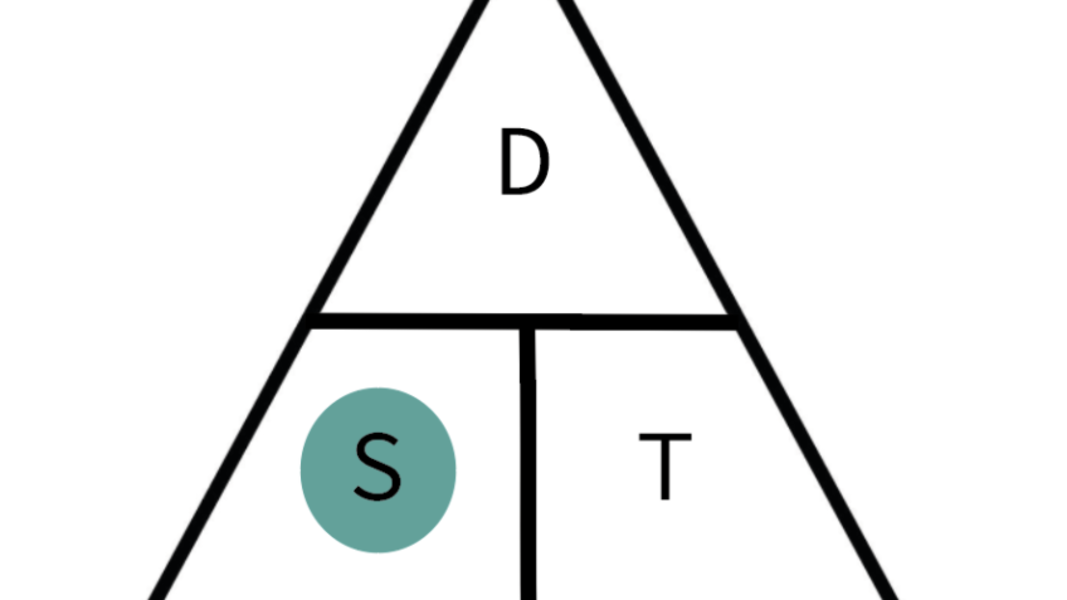
To calculate speed, you need to divide the distance by the time. You can work this out by using the triangle. If you cover up speed, you are left with distance over time.

Here is an example:

If a driver has travelled 180 miles and it took them 3 hours to make that distance, then to work out their speed you would take:

180 miles / 3 hours -\> 180 / 3 = 60

So the driver’s speed would be 60mph.

How to calculate distance

To work out the distance travelled, you will need to multiply speed and time.

If a driver travelled at 100mph for 4 hours, then to work out the distance you will need to multiply the speed with the time.

100mph x 4 hours -\> 100 x 4 = 400

The distance is 400 miles.

How to calculate the time

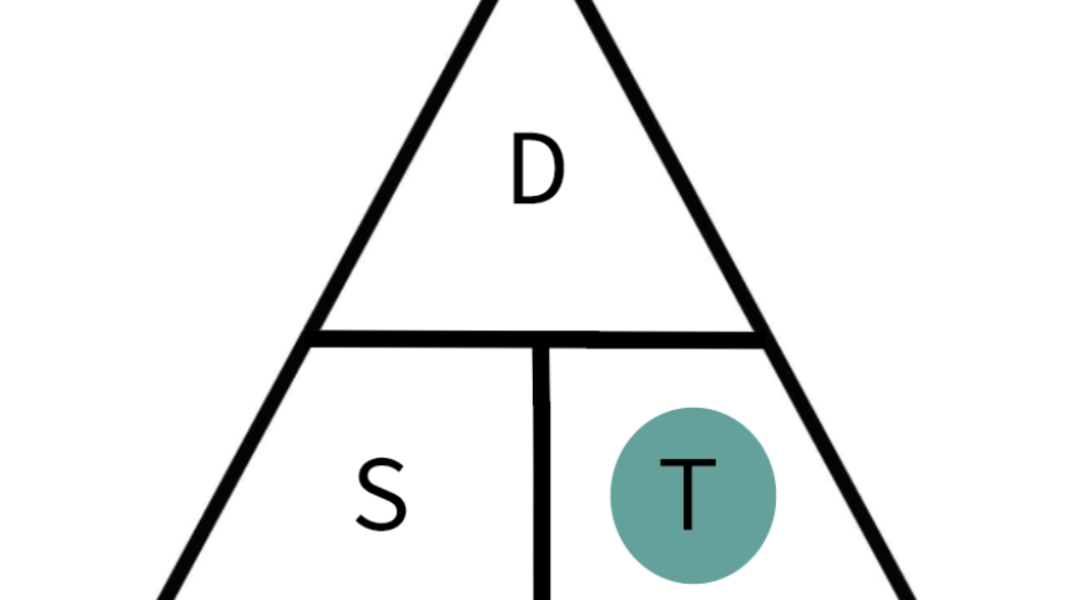
To work out the time that the journey took, you will need to know the speed of the journey and the distance that was travelled.

If the driver travelled 50 miles at 5mph, then to work out the time taken you would divide:

50miles / 5 miles per hour -\> 50 / 5 = 10

The time taken to travel this distance is 10 miles per hour.

Three example speed/distance/time questions

• Andy drives his lorry for 400 miles, which takes him 8 hours. Harry drives 200 miles, which takes him 4.5 hours. Who is travelling faster?

Answer: Andy is driving at 50mph, and Harry is driving at 44.44mph. So, Andy is driving faster.

• Tessa runs a 5km race with her running club every Saturday. She runs this in 40 minutes. If she maintains the same speed, how long would it take her to run the 8km race?

Answer: Her speed is 7.5kph. If she runs 10km at 7.5kph, to work out the time, you need to divide 8 by 7.5, which equals 1.066. If we convert this into hours and minutes, it will take her 1 hour and 4 minutes to run 8km.

• Hannah goes on a cycling trip. In the first half of the journey, she travels at 10mph for 2 hours. In the second half, she travels at 20mph for 90 minutes. How far does she travel in total?

Answer: In the first half of her journey she travels 20 miles (10 x 2 = 20). In the second half, she travels 30 miles, (20 x 1.5 = 30). 20+30 =50, so she travels 50 miles in total.

Methods to get better at these questions

To improve your skill in answering speed distance time questions, there are two main things you can do.

First, make sure that you are familiar with the formula triangle. The key to answering these questions is knowing the formula inside out, so that you always know what equation to use, whether the exam question is asking you to work out speed or distance.

By making sure you have memorized the formula in all its variations, you will save yourself time when answering questions.

Secondly, you should focus on improving your general mathematical skills. You may get a compound question, which asks you to use the formula in conjunction with other maths skills to work out the answer to the problem.

You can try a few maths practice tests, such as these , which will help you to practise your basic numeracy skills.

Enjoy what you’ve read? Let others know!

• Share on whatsapp
• Share on linkedin
• Share on twitter
• Share on facebook
• Share via email

By using our website you agree with our Cookie Policy.

Speed Distance Time Calculator

Please enter the speed and distance values to calculate the travel time in hours, minutes and seconds.

About Speed Distance Time Calculator

This online calculator tool can be a great help for calculating time basing on such physical concepts as speed and distance. Therefore, in order to calculate the time, both distance and speed parameters must be entered. For the speed , you need to enter its value and select speed unit by using the scroll down menu in the calculator. For distance , you should enter its value and also select the proper length measurement unit from the scroll down menu. You'll receive the result in standard time format (HH:MM:SS).

Time Speed Distance Formula

Distance is equal to speed × time. Time is equal Distance/Speed.

Calculate Time from Distance and Speed Examples

Recent comments.

Going 65mph for 30 seconds how far would you get? None of these formulas work without distance. How would I find the distance from time and speed?

if i travel 0.01 inches per second and I need to travel 999999999 kilometers, it takes 556722071 Days and 20:24:34 WHAT

4. How long does it take to do 100m at 3kph ? No I thought you would just divide 100 ÷ 3 = which 33.33333 so 33 seconds or so I thought. But apparently it 2 mins.

This was the best tool ive ever used that was on point from speed to distance and time Calculator

This was somewhat unhelpful as I know the time and distance, but not the speed. Would be helpful if this calculator also could solve the other two as well.

If a total distance of 2 miles is driven, with the first mile being driven at a speed of 15mph, and the second mile driven at a speed of 45 mph: What is the average speed of the full 2 mile trip?

hi sorry im newly introduced to this and i dont understand how to use it but in need to find the distance if i was travelling in the average speed of 15km/hr in 4 hours how far would i travel

D= 697 km T= 8 hours and 12 minutes S= ?

if a train is going 130 miles in 50 minutes, how fast is it going in miles per hour ??

whats the speed if you travel 2000 miles in 20hours?

How long would it take me to drive to Mars at 100 miles per hour and how much gas would I use in a 2000 Ford Mustang000000/ Also, how much CO2 would I release into the air?

great tool helped me alot

A car can go from rest to 45 km/hr in 5 seconds. What is its acceleration?

Guys how much time will a cyclist take to cover 132 METRES With a speed of 8 km/ph

@Mike Depends on how fast that actually is. For every 10 mph above 60, but below 120, you save 5 seconds a mile. But between the 30-60 area, every ten saves 10 seconds a mile (if I am remembering correctly), and every 10 between 15-30 is 20 seconds. Realistically, it isn't likely isn't worth it, unless it is a relatively straight drive with no stops, in which case you will likely go up a gear for the drive and thus improve gas efficiency for the trip. Only really saves time if it is over long trips 300+ miles (in which case, assuming you were on the interstate) that 5 seconds a mile would save you 25 minutes from the drive, making it go from 4h35m to 4h10m. For me, I have family across the U.S., so family visits are usually 900-1400 miles. Even only driving 5 above usually saves me 90-150 minutes or so (since I often have stretches where I drive on US highways which have 55 mph speed limits)

I would like to know if driving fast is worth it for short trips. If I drive 10 MPH over the speed limit for 10 miles, how much time do i save ? Is there an equation for that ?

it helps me in lot of stuff

awesome, helped me notice how long my taiga (electric seedoo) is going to last.

Very good! This helped me a lot.

Home / United States / Math Classes / Formulas / Distance Speed Time Formulas

Distance Speed Time Formulas

This article explores the formula describing the relationship between distance, speed and time. If the values of any two of the three quantities, among speed, distance or time are given, the formula can be used to find the third quantity. ...Read More Read Less

Formula for Speed, Distance and Time

Distance is the numerical measure of how far a point or an object is from another point or object. Time is the measure of the time taken for an entity to reach from one point to another. Lastly, the measure of how fast or slow an object or a point moves is known as speed.

Speed, distance and time are related to each other by the formula:

Speed = \(\frac{\text{Distance}}{\text{Time}}\)

So, speed can be defined as the distance traveled per unit time. It indicates the rate at which an object moves between two points. The formula connecting speed, distance and time can also be given as:

\(x=\frac{d}{t}\)

\(x\) = Speed

\(d\) = Distance traveled

\(t\) = Time taken

Distance is measured in units of length like meters, kilometers, miles and other units like feet or inches. Time is measured in seconds, minutes and hours. Speed is measured in distance per unit time, for example, meters per second (m/s), kilometers per hour (km/hour), or miles per hour.

The above formula can also be used to determine distance or time.

• Distance = Speed \(\times\) Time (or) \(d\ =\ x\ \times\ t\)
• Time = \(\frac{\text{Distance}}{\text{Speed}} = \frac{d}{x}\)

Therefore, distance is the product of speed and time, and time is distance per unit speed.

Rapid Recall

Solved Examples

Example 1: Laura was going to the mall from her house in her car at an average speed of 36 mph. She took 0.2 hours to reach the mall. Calculate the distance she traveled from her house to the mall?

Solution: Speed of the car, \(x\) = 36 mph

Time taken by the car to reach the mall, \(t\) = 0.2 hr

We need to find the distance covered by Laura.

The formula relating speed, distance and time is,

Distance traveled, \(d=x \times t\)

\(d=36 \times 0.2\)  Substitute 36 for \(x\) and 0.2 for \(t\)

   \(=7.2\)           Multiply

Therefore the distance traveled by Laura from her house to the mall is 7.2 miles.

Example 2: Ronald covered a distance of 280 miles in 4 hours on his motorbike. Calculate how fast the bike would have moved to cover this distance.

Distance covered, \(d\) = 280 miles,

Time taken, \(t\) = 4 hours

\(x=\frac{d}{t}\)     Formula for speed

\(x =\frac{280}{4}\)  Substitute 280 for d and 4 for \(t\)

\(x=70\)    Divide

Therefore, the bike would have moved at a speed of 70 miles per hour to cover a distance of 280 miles.

Example 3: In a cycle race, cyclist A is moving with a speed of 2 km/hr and cyclist B is moving at a speed of 3 km/hr. The cyclists need to cover a distance of 12 km to reach the destination. Which cyclist will reach the destination first?

Solution: To determine which cyclist reaches the destination, first, we need to compare the time taken by each cyclist to reach the destination.

Speed of cyclist A, \(x_a\) = 2 km/hr

Speed of cyclist B, \(x_b\) = 3 km/hr

Distance covered by both the cyclists, \(d\) = 12 km

We need to find the time taken by cyclist A and cyclist B.

\(t=\frac{d}{x}\)              Formula for time taken

\(t_a = \frac{12}{2}=6\)    Substitute 12 for \(d\) and 2 for \(x\) and solve

\(t_b = \frac{12}{3}=4\)    Substitute 12 for \(d\) and 3 for \(x\) and solve

So the time taken by cyclist A is 6 hours and the time taken by cyclist B is 4 hours.

Now since 6 hours is greater than 4 hours, that is, cyclist B takes less time to reach the destination.

Therefore cyclist B will reach the destination first.

What is the definition of speed?

The rate of change of the position of an object in any direction is called the speed of the object.

What is the definition of time?

The ratio of distance traveled or covered by an object to its unit speed is defined as time.

What is the definition of distance?

Distance is the numerical measure of how far a point or an object is from another point or object. Distance is calculated as the product of speed and time.

For a given speed if the distance is doubled then what will be the change in time taken?

For a given speed, if the distance is doubled then the time taken will also be doubled.

Check out our other courses

Grades 1 - 12

Level 1 - 10

Travel Time Calculator

Introduction.

In the fast-paced world of travel and transportation, optimizing the time spent on journeys is essential. The Travel Time Calculator emerges as a handy tool, offering a swift solution to estimate travel durations. Whether planning a road trip, commuting, or scheduling flights, this calculator proves invaluable for individuals seeking accurate and efficient travel time predictions.

The Travel Time Calculator relies on a simple formula to determine the duration of a journey. The formula is expressed as:

Travel Time=Distance Speed Travel Time = Speed Distance ​

Here, the distance represents the length of the journey, and the speed denotes the average speed at which the travel occurs. The result is the estimated time required to cover the specified distance.

How to Use?

Utilizing the Travel Time Calculator is a straightforward process. Follow these steps to obtain quick and accurate travel time estimates:

• Enter Distance : Input the distance of your journey. This could be in miles, kilometers, or any other relevant unit.
• Specify Average Speed : Enter the average speed at which you anticipate traveling. This speed should reflect the overall pace of your journey, considering factors such as speed limits and road conditions.
• Click Calculate or Submit : Most calculators feature a button to initiate the computation. Clicking this button will generate the estimated travel time based on the provided distance and speed.
• Review the Output : The calculator will display the estimated travel time, allowing you to plan your schedule with precision.

Consider a road trip covering a distance of 300 miles, with an anticipated average speed of 60 miles per hour. Using the Travel Time Calculator, the estimated travel time would be calculated as follows:

Travel Time=300 miles60 mph=5 hours  Travel Time = 60 mph 300 miles ​ = 5 hours

Q: Can the Travel Time Calculator account for variations in speed during a journey? A: The calculator provides an average travel time based on the entered average speed. For more detailed calculations, consider segmenting the journey into different legs with varying speeds.

Q: Is the Travel Time Calculator suitable for air travel? A: While the calculator primarily focuses on ground travel, it can provide rough estimates for air travel based on the average speed of the flight.

Q: Does the calculator consider factors like traffic and stops? A: The Travel Time Calculator offers a basic estimate and may not account for variables like traffic, stops, or delays. It’s advisable to use it as a planning tool and adjust for real-time conditions.

Conclusion:

The Travel Time Calculator is a valuable companion for anyone planning journeys, whether for business or leisure. By providing quick and reliable estimates, it facilitates effective time management and helps individuals make informed decisions about their travel schedules. Embracing this calculator empowers travelers to plan their trips with confidence, ensuring they reach their destinations on time and with minimal hassle.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Einstein's equation and time travel

How is Einstein's equation (Gμν = 8πG Tμν) actually applied? And how does it support the theory of time travel.

Many physicists refer to this as Einstein’s Equations (plural) because it's actually a set of several equations. The symbol Gμν denotes the "Einstein tensor," which is a measure of how much space-time is curving. The symbol Tμν denotes the "energy momentum tensor," which measures the density and flux of the energy and momentum of matter. The energy and momentum of matter causes space-time to curve in a way that is described by Einstein’s Equations. The curvature of space-time is what causes all the effects that we associate with "gravity."

There are many textbooks that explain how to apply Einstein’s Equations equations to various situations, but they require a very advanced background in physics and mathematics. I will therefore have to summarize things in words.

Before talking about time travel, let me first explain what a "world-line" is. Suppose that an object at a particular time is sitting at some particular point in space. At another time, it will be sitting at another point. Its locations at different times trace out a path through space-time, which is called the object’s world line. This path extends forward to points farther and farther in the future (until the object ceases to exist for some reason, at which point its world-line ends). But imagine that an object’s world-line bends around in a loop, so that at it arrives at a point in space-time where it had already been? For example, there may be a point on my world line that was me at my fifth birthday party at my parents’ home in New York City. Another point (farther along my world-line) is me now, aged 61, sitting in my office at the University of Delaware. If I continue farther and farther along my world line, might I end up again at my fifth birthday party in New York City in 1958? Could my five-year old self meet my much older self at that party? That is what most people mean by "time travel." In the jargon of physics, such a world line that bent around and intersected itself is called a "closed time-like loop" or "closed time-like curve."

The question is whether world-lines that are closed time-like loops are possible in the real world. It is comparatively easy to show that if space-time were not curved world-lines would definitely not be able to bend around to form closed time-like loops. But one might hope that gravity, by curving space-time, could bend some world-lines around to make closed loops. The way people have studied this question is to assume that Einstein’s equations correctly describe how the energy and momentum of matter curves space-time. Then they look for solutions of those equations where space-time curves in such a way as to make closed time-like loops possible, and therefore time-travel possible. No one has ever found such solutions. People have on occasion found what seemed to be such solutions, but on closer inspection it was found that when realistic conditions are imposed, no time travel is possible. An example is the Gödel Universe (or Gödel metric).

One kind of solution that would allow time travel is called a "Minkowski wormhole." A Minkowski wormhole would be like a tunnel that took you from one point in space-time to what seemed like a far distant point--a point far away in space, or in the past, or in the future. But people have shown that for a Minkowski wormhole to exist, there would have to be a type of matter whose energy and momentum were unlike any kind of matter ever seen and extremely unlikely to exist in the real world.

The great majority of experts believe that time travel is not allowed by the laws of physics. But no one has proved that rigorously. If you want to learn more, you could try to find discussions of closed time-like loops and Minkowski wormholes in books or on the internet.

-Stephen Barr

• General relativity

Navigation menu

Page actions.

• View source

Personal tools

• Recent changes
• Random page
• Help about MediaWiki
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information

• This page was last edited on 18 May 2015, at 21:41.
• Privacy policy
• Disclaimers

The Time to Travel a Distance under Constant Acceleration calculator compute the time required to travel a distance (x) from rest based on a constant acceleration (a).

INSTRUCTIONS: Choose units and enter the following:

• ( x ) Distance Traveled
• ( a ) Constant Acceleration

Time to Travel(t): The calculator returns the time in seconds.  However, this can be automatically converted into compatible units via the pull-down menu.

The Math / Science

The formula for the time required to travel a distance under constant acceleration is:

    `t = sqrt( (2*x)/a)`

• t is the time of travel under constant acceleration
• x is the distance traveled 
• a is the constant acceleration

Related Calculators:

• Compute the time from the distance and velocity .
• Compute the velocity from the distance and time .
• Compute the distance from the velocity and time .
• Distance from initial displacement, velocity and time
• Distance from initial displacement, velocity, time and constant acceleration

Sorry, JavaScript must be enabled. Change your browser options, then try again .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Seismic Reflection (Single Layer)

• Last updated
• Save as PDF
• Page ID 3541

• Magali Billen
• University of California, Davis

Reflection surveys follow the same basic principles as refraction surveys, except of course they use reflected waves instead of refracted waves. We can use reflected waves to get h and v 1 , but we cannot get v 2 unless we have a reflection from a deeper layer.

If there are multiple layers, we can determine each layers data such as height and velocity by working down one layer at a time. However, today we will only focus on a single layer subsurface. We can use the layer geometry to get a travel-time equation.

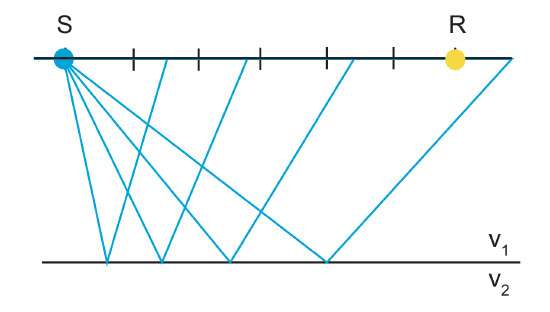
In the case of reflection, we can have v 2 >v 1 or v 2 <v 1 , we will get a reflected wave either way.

Starting with our distance equation,

\[d=v\cdot t\]

\[t=\frac{d}{v}\]

\[d^2=(\frac{x}{2})^2+h^2\]

The total distance a reflected wave will travel is 2d, because the wave must go down and then back up to the receiver.

\[2d=2((\frac{x}{2})^2+h^2)^{\frac{1}{2}}\]

\[2d=(x^2+4h^2)^{\frac{1}{2}}\]

\[t=\frac{2d}{v_1}\]

\[t=\frac{\sqrt{x^2+4h^2}}{v_1}\]

What is the intercept time?

t(x=0)=t o =\(\frac{2h}{v_1}\)

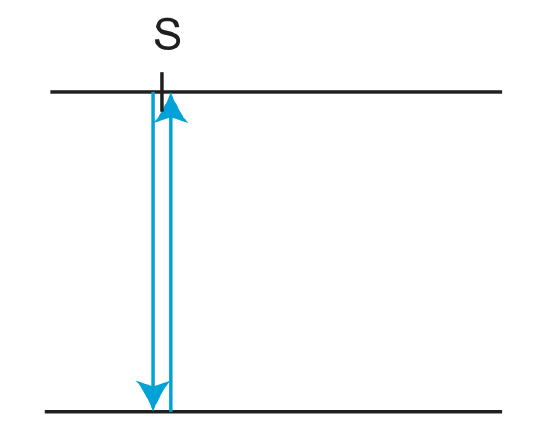
For a vertically reflected wave, if you know v 1 , you can get h.

\[h=\frac{v_1t_o}{2}\]

We've just said that calculating h from a vertically reflected wave is easy if you know v 1 . So how do we get v 1 ? We are going to assume that we can't measure the direct wave (this is not usually true for layer 1, but definitely true for deeper layers-there is no direct wave here).

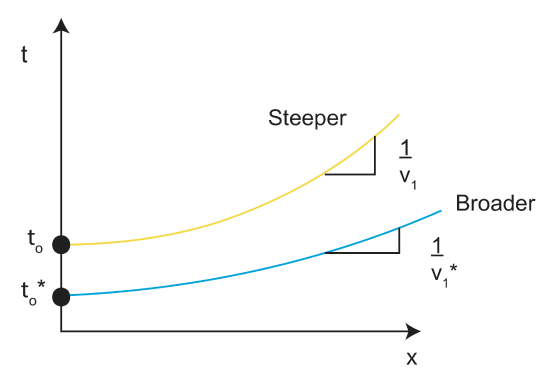
From the last section, we know that the graph of a refracted wave is a line. So what is the shape of t(x) for a reflected wave?

Figure \(\PageIndex{4}\): Vertically Reflected Wave

\[t^2=\frac{x^2}{v_1^2}+\frac{4h^2}{v_1^2}\]

We know that \(\frac{4h^2}{v_1^2}\) can also be written as t o 2 .

\[t_o^2=t^2-\frac{x^2}{v_1^2}\]

\[1=\frac{t^2}{t_o^2}-\frac{x^2}{v_1^2t_o^2}\]

The above equation is the equation for a hyperbola where a=t o and b=v 1 t o . The intercept is at t o . The slope at large x=\(\frac{a}{b}=\frac{t_o}{v_1t_o}=\frac{1}{v_1}\).

We can derive that the equation for t o is:

\[t_o=\frac{2h}{v_1}\]

The figure below shows how the hyperbola changes with layer thickness. The hyperbola will increase with increasing layer thickness.

What if two layers have the same thickness but different velocities?

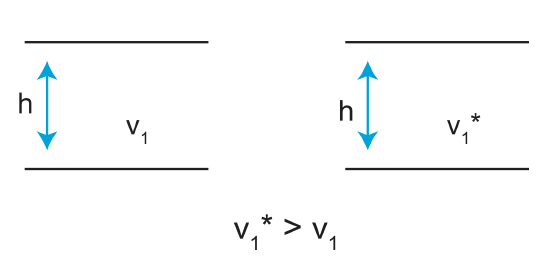
In the above figure, v 1 * >v 1 . Using our equation \(t_o=\frac{2h}{v_1}\), t o \(\downarrow\) for v 1 \(\uparrow\). Since the slope of the hyperbola \(\frac{a}{b}\) is \(\frac{1}{v_1}\), we can see that as v 1 increases, we will get a lower slope (a broader shape).

In the case of multiple layers, the travel time equation is also a hyperbola. We just used a single layer example to understand the basic concepts. Now that we have a basic understanding of the different terms and how the data can be graphed, we are going to analyze it using a method called Normal Move-out (NMO).

\[T_{NMO}=t(x)-t_o\]

The equation for T NMO gives us the "shape of the hyperbola". If we could correct for NMO, all reflections would look like they come from a vertical reflection. As you 'move-out' along the hyperbola, the path the ray takes gets longer and longer. Thus by correcting for NMO, we are looking at data close to the first few recievers, ie those that have taken shorter paths and have not 'moved-out'.

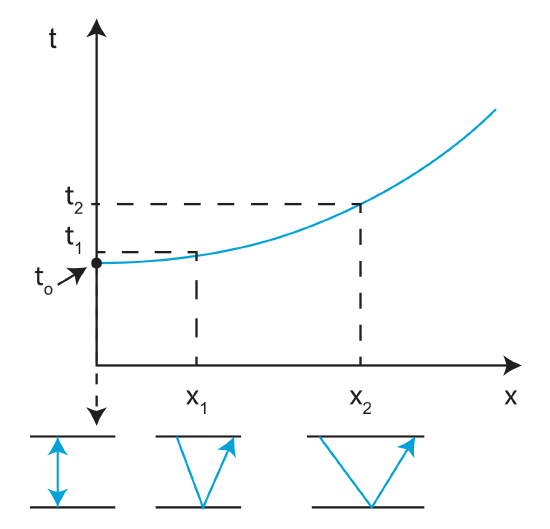
At small x, we can approximate

\[t(x)\approx t_o+\frac{x}{2v_1^2t_o}\]

\[t(x)^2=t_o^2+\frac{x^2}{v_1^2}\]

Using binomial expansion, we get that

\[t(x)=t_o(1+(\frac{x^2}{v_1t_o})^2)^{\frac{1}{2}}\]

Substituting for t(x):

\[T_{NMO}\approx\frac{x^2}{2v_1^2t_o}\]

Solve for v 1

\[v_1\approx\frac{x}{\sqrt{2t_oT_{NMO}}}\]

When you are actually analyzing a travel time graph, there are several steps you can take to get information on the subsurface.

• Measure (or read off) t o , t(x), and x
• If x has a small value, calculate T NMO =t(x)-t o
• Calculate \(v_1\approx\frac{x}{\sqrt{2t_oT_{NMO}}}\)
• Calculate \(h=\frac{v_1t_o}{2}\)

For real processing of reflection data

• We guess v 1 and h
• Calculate predicted NMO
• Correct arrivals
• Are they flat? If not, try new values (loop through many values and find peak sum)

A beginner's guide to time travel

Learn exactly how Einstein's theory of relativity works, and discover how there's nothing in science that says time travel is impossible.

Everyone can travel in time . You do it whether you want to or not, at a steady rate of one second per second. You may think there's no similarity to traveling in one of the three spatial dimensions at, say, one foot per second. But according to Einstein 's theory of relativity , we live in a four-dimensional continuum — space-time — in which space and time are interchangeable.

Einstein found that the faster you move through space, the slower you move through time — you age more slowly, in other words. One of the key ideas in relativity is that nothing can travel faster than the speed of light — about 186,000 miles per second (300,000 kilometers per second), or one light-year per year). But you can get very close to it. If a spaceship were to fly at 99% of the speed of light, you'd see it travel a light-year of distance in just over a year of time. 

That's obvious enough, but now comes the weird part. For astronauts onboard that spaceship, the journey would take a mere seven weeks. It's a consequence of relativity called time dilation , and in effect, it means the astronauts have jumped about 10 months into the future. 

Traveling at high speed isn't the only way to produce time dilation. Einstein showed that gravitational fields produce a similar effect — even the relatively weak field here on the surface of Earth . We don't notice it, because we spend all our lives here, but more than 12,400 miles (20,000 kilometers) higher up gravity is measurably weaker— and time passes more quickly, by about 45 microseconds per day. That's more significant than you might think, because it's the altitude at which GPS satellites orbit Earth, and their clocks need to be precisely synchronized with ground-based ones for the system to work properly. 

The satellites have to compensate for time dilation effects due both to their higher altitude and their faster speed. So whenever you use the GPS feature on your smartphone or your car's satnav, there's a tiny element of time travel involved. You and the satellites are traveling into the future at very slightly different rates.

But for more dramatic effects, we need to look at much stronger gravitational fields, such as those around black holes , which can distort space-time so much that it folds back on itself. The result is a so-called wormhole, a concept that's familiar from sci-fi movies, but actually originates in Einstein's theory of relativity. In effect, a wormhole is a shortcut from one point in space-time to another. You enter one black hole, and emerge from another one somewhere else. Unfortunately, it's not as practical a means of transport as Hollywood makes it look. That's because the black hole's gravity would tear you to pieces as you approached it, but it really is possible in theory. And because we're talking about space-time, not just space, the wormhole's exit could be at an earlier time than its entrance; that means you would end up in the past rather than the future.

Trajectories in space-time that loop back into the past are given the technical name "closed timelike curves." If you search through serious academic journals, you'll find plenty of references to them — far more than you'll find to "time travel." But in effect, that's exactly what closed timelike curves are all about — time travel

This article is brought to you by  How It Works .

How It Works is the action-packed magazine that's bursting with exciting information about the latest advances in science and technology, featuring everything you need to know about how the world around you — and the universe — works.

There's another way to produce a closed timelike curve that doesn't involve anything quite so exotic as a black hole or wormhole: You just need a simple rotating cylinder made of super-dense material. This so-called Tipler cylinder is the closest that real-world physics can get to an actual, genuine time machine. But it will likely never be built in the real world, so like a wormhole, it's more of an academic curiosity than a viable engineering design.

Yet as far-fetched as these things are in practical terms, there's no fundamental scientific reason — that we currently know of — that says they are impossible. That's a thought-provoking situation, because as the physicist Michio Kaku is fond of saying, "Everything not forbidden is compulsory" (borrowed from T.H. White's novel, "The Once And Future King"). He doesn't mean time travel has to happen everywhere all the time, but Kaku is suggesting that the universe is so vast it ought to happen somewhere at least occasionally. Maybe some super-advanced civilization in another galaxy knows how to build a working time machine, or perhaps closed timelike curves can even occur naturally under certain rare conditions.

This raises problems of a different kind — not in science or engineering, but in basic logic. If time travel is allowed by the laws of physics, then it's possible to envision a whole range of paradoxical scenarios . Some of these appear so illogical that it's difficult to imagine that they could ever occur. But if they can't, what's stopping them? 

Thoughts like these prompted Stephen Hawking , who was always skeptical about the idea of time travel into the past, to come up with his "chronology protection conjecture" — the notion that some as-yet-unknown law of physics prevents closed timelike curves from happening. But that conjecture is only an educated guess, and until it is supported by hard evidence, we can come to only one conclusion: Time travel is possible.

A party for time travelers 

Hawking was skeptical about the feasibility of time travel into the past, not because he had disproved it, but because he was bothered by the logical paradoxes it created. In his chronology protection conjecture, he surmised that physicists would eventually discover a flaw in the theory of closed timelike curves that made them impossible. 

In 2009, he came up with an amusing way to test this conjecture. Hawking held a champagne party (shown in his Discovery Channel program), but he only advertised it after it had happened. His reasoning was that, if time machines eventually become practical, someone in the future might read about the party and travel back to attend it. But no one did — Hawking sat through the whole evening on his own. This doesn't prove time travel is impossible, but it does suggest that it never becomes a commonplace occurrence here on Earth.

The arrow of time 

One of the distinctive things about time is that it has a direction — from past to future. A cup of hot coffee left at room temperature always cools down; it never heats up. Your cellphone loses battery charge when you use it; it never gains charge. These are examples of entropy , essentially a measure of the amount of "useless" as opposed to "useful" energy. The entropy of a closed system always increases, and it's the key factor determining the arrow of time.

It turns out that entropy is the only thing that makes a distinction between past and future. In other branches of physics, like relativity or quantum theory, time doesn't have a preferred direction. No one knows where time's arrow comes from. It may be that it only applies to large, complex systems, in which case subatomic particles may not experience the arrow of time.

Time travel paradox 

If it's possible to travel back into the past — even theoretically — it raises a number of brain-twisting paradoxes — such as the grandfather paradox — that even scientists and philosophers find extremely perplexing.

Killing Hitler

A time traveler might decide to go back and kill him in his infancy. If they succeeded, future history books wouldn't even mention Hitler — so what motivation would the time traveler have for going back in time and killing him?

Killing your grandfather

Instead of killing a young Hitler, you might, by accident, kill one of your own ancestors when they were very young. But then you would never be born, so you couldn't travel back in time to kill them, so you would be born after all, and so on … 

A closed loop

Suppose the plans for a time machine suddenly appear from thin air on your desk. You spend a few days building it, then use it to send the plans back to your earlier self. But where did those plans originate? Nowhere — they are just looping round and round in time.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

How It Works has a special formula for making learning fun by answering questions on science, space, history, technology, transport and the environment with engaging articles, in-depth special features, global science news, and topical interviews. With impressive cutaway illustrations that show how things function, and mindblowing photography of the planet’s most inspiring spectacles, How It Works represents the pinnacle of engaging, factual fun for a mainstream audience keen to keep up with the latest tech and the most impressive phenomena on the planet and beyond. Written and presented in a style that makes even the most complex subjects interesting and easy to understand, How It Works is enjoyed by readers of all ages.

Get fantastic offers by subscribing to the digital and/or print edition now. Subscribers get 13 issues per year!

See the explosive 'devil comet' get its tail ripped off by a solar storm days before its close approach to the sun

Global 'time signals' subtly shifted as the total solar eclipse reshaped Earth's upper atmosphere, new data shows

Packs of dog-shaped robots could one day roam the moon — if they can find their footing on Earth first

Most Popular

• 2 James Webb telescope confirms there is something seriously wrong with our understanding of the universe
• 3 NASA spacecraft snaps mysterious 'surfboard' orbiting the moon. What is it?
• 4 'Exceptional' prosthesis of gold, silver and wool helped 18th-century man live with cleft palate
• 5 AI pinpoints where psychosis originates in the brain
• 2 Scientists are one step closer to knowing the mass of ghostly neutrinos — possibly paving the way to new physics
• 3 50-foot 'king of the serpents' may have been the biggest snake to ever live
• 4 Giant, 82-foot lizard fish discovered on UK beach could be largest marine reptile ever found
• 5 NASA's downed Ingenuity helicopter has a 'last gift' for humanity — but we'll have to go to Mars to get it

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Time Dilation

• Last updated
• Save as PDF
• Page ID 4515

Learning Objectives

By the end of this section, you will be able to:

• Explain how time intervals can be measured differently in different reference frames.
• Describe how to distinguish a proper time interval from a dilated time interval.
• Describe the significance of the muon experiment.
• Explain why the twin paradox is not a contradiction.
• Calculate time dilation given the speed of an object in a given frame.

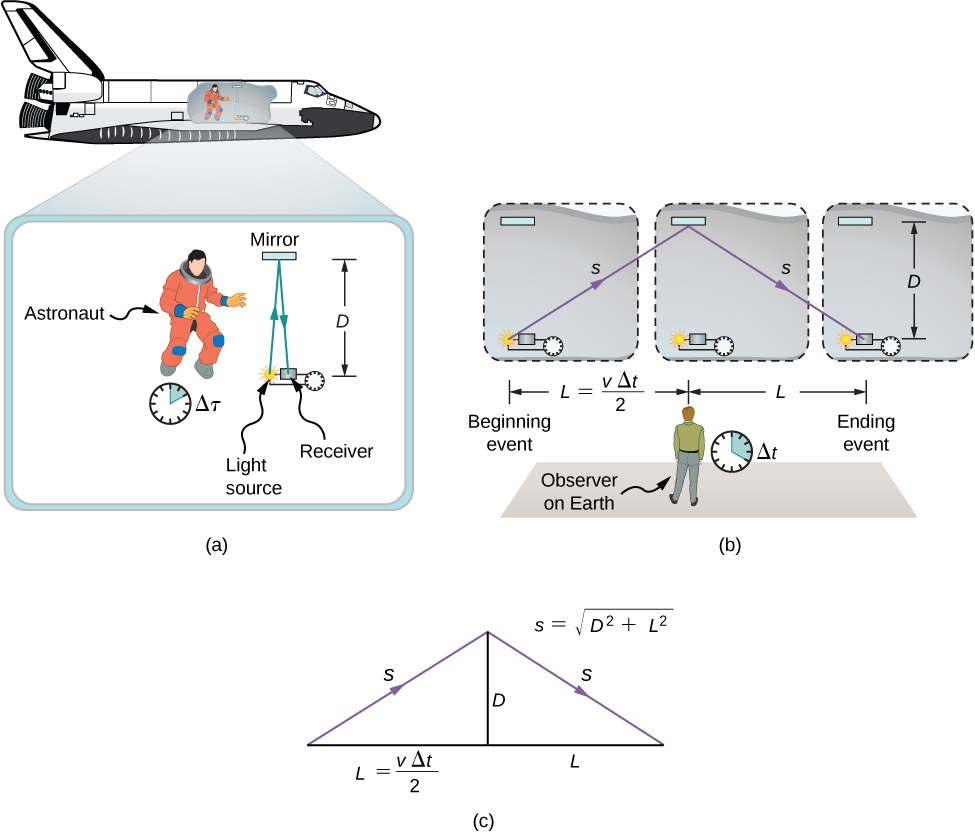
The analysis of simultaneity shows that Einstein’s postulates imply an important effect: Time intervals have different values when measured in different inertial frames. Suppose, for example, an astronaut measures the time it takes for a pulse of light to travel a distance perpendicular to the direction of his ship’s motion (relative to an earthbound observer), bounce off a mirror, and return (Figure \(\PageIndex{1a}\)). How does the elapsed time that the astronaut measures in the spacecraft compare with the elapsed time that an earthbound observer measures by observing what is happening in the spacecraft?

Examining this question leads to a profound result. The elapsed time for a process depends on which observer is measuring it. In this case, the time measured by the astronaut (within the spaceship where the astronaut is at rest) is smaller than the time measured by the earthbound observer (to whom the astronaut is moving). The time elapsed for the same process is different for the observers, because the distance the light pulse travels in the astronaut’s frame is smaller than in the earthbound frame, as seen in Figure \(\PageIndex{1b}\). Light travels at the same speed in each frame, so it takes more time to travel the greater distance in the earthbound frame.

Definition: Time Dilation

Time dilation is the lengthening of the time interval between two events for an observer in an inertial frame that is moving with respect to the rest frame of the events (in which the events occur at the same location).

To quantitatively compare the time measurements in the two inertial frames, we can relate the distances in Figure \(\PageIndex{1b}\) to each other, then express each distance in terms of the time of travel (respectively either \(\Delta t\) or \(\Delta \tau\)) of the pulse in the corresponding reference frame. The resulting equation can then be solved for \(\Delta t\) in terms of \(\Delta \tau\).

The lengths \(D\) and \(L\) in Figure \(\PageIndex{1c}\) are the sides of a right triangle with hypotenuse \(s\). From the Pythagorean theorem ,

\[s^2 = D^2 + L^2. \nonumber \]

The lengths \(2s\) and \(2L\) are, respectively, the distances that the pulse of light and the spacecraft travel in time \(\Delta t\) in the earthbound observer’s frame. The length \(D\) is the distance that the light pulse travels in time \(\Delta \tau\) in the astronaut’s frame. This gives us three equations:

\[\begin{align*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2D &= c\Delta \tau. \end{align*} \nonumber \]

Note that we used Einstein’s second postulate by taking the speed of light to be c in both inertial frames. We substitute these results into the previous expression from the Pythagorean theorem:

\[ \begin{align*} s^2 &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*} \nonumber \]

Then we rearrange to obtain

\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^2. \nonumber \]

Finally, solving for \(\Delta t\) in terms of \(\Delta \tau\) gives us

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (v/c)^2}}. \nonumber \]

This is equivalent to

\[\Delta t = \gamma \Delta \tau, \label{timedilation} \]

where \(\gamma\) is the relativistic factor (often called the Lorentz factor ) given by

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \nonumber \]

and \(v\) and \(c\) are the speeds of the moving observer and light, respectively.

Note the asymmetry between the two measurements. Only one of them is a measurement of the time interval between two events—the emission and arrival of the light pulse—at the same position. It is a measurement of the time interval in the rest frame of a single clock. The measurement in the earthbound frame involves comparing the time interval between two events that occur at different locations. The time interval between events that occur at a single location has a separate name to distinguish it from the time measured by the earthbound observer, and we use the separate symbol \(\Delta \tau\) to refer to it throughout this chapter.

Definition: Proper Time

The proper time interval \(\Delta \tau\) between two events is the time interval measured by an observer for whom both events occur at the same location.

The equation relating \(\delta t\) and \(\Delta \tau\) is truly remarkable. First, as stated earlier, elapsed time is not the same for different observers moving relative to one another, even though both are in inertial frames. A proper time interval \(\Delta \tau\) for an observer who, like the astronaut, is moving with the apparatus, is smaller than the time interval for other observers. It is the smallest possible measured time between two events. The earthbound observer sees time intervals within the moving system as dilated (i.e., lengthened) relative to how the observer moving relative to Earth sees them within the moving system. Alternatively, according to the earthbound observer, less time passes between events within the moving frame. Note that the shortest elapsed time between events is in the inertial frame in which the observer sees the events (e.g., the emission and arrival of the light signal) occur at the same point.

This time effect is real and is not caused by inaccurate clocks or improper measurements. Time-interval measurements of the same event differ for observers in relative motion. The dilation of time is an intrinsic property of time itself. All clocks moving relative to an observer, including biological clocks, such as a person’s heartbeat, or aging, are observed to run more slowly compared with a clock that is stationary relative to the observer.

Note that if the relative velocity is much less than the speed of light (v << c), then \(v^2/c^2\) is extremely small, and the elapsed times \(\Delta t\) and \(\Delta \tau\) are nearly equal. At low velocities, physics based on modern relativity approaches classical physics—everyday experiences involve very small relativistic effects. However, for speeds near the speed of light, \(v^2/c^2\) is close to one, so \(\sqrt{1 - v^2/c^2}\) is very small and \(\Delta t\) becomes significantly larger than \(\Delta \tau\).

Half-Life of a Muon

There is considerable experimental evidence that the equation \(\Delta t = \gamma \Delta \tau\) is correct. One example is found in cosmic ray particles that continuously rain down on Earth from deep space. Some collisions of these particles with nuclei in the upper atmosphere result in short-lived particles called muons . The half-life (amount of time for half of a material to decay) of a muon is 1.52 μs when it is at rest relative to the observer who measures the half-life. This is the proper time interval \(\Delta \tau\). This short time allows very few muons to reach Earth’s surface and be detected if Newtonian assumptions about time and space were correct. However, muons produced by cosmic ray particles have a range of velocities, with some moving near the speed of light. It has been found that the muon’s half-life as measured by an earthbound observer (\(\Delta t\)) varies with velocity exactly as predicted by the equation \(\Delta t = \gamma \Delta \tau\). The faster the muon moves, the longer it lives. We on Earth see the muon last much longer than its half-life predicts within its own rest frame. As viewed from our frame, the muon decays more slowly than it does when at rest relative to us. A far larger fraction of muons reach the ground as a result.

Before we present the first example of solving a problem in relativity, we state a strategy you can use as a guideline for these calculations.

PROBLEM-SOLVING STRATEGY: RELATIVITY

• Make a list of what is given or can be inferred from the problem as stated (identify the knowns). Look in particular for information on relative velocity v .
• Identify exactly what needs to be determined in the problem (identify the unknowns).
• Make certain you understand the conceptual aspects of the problem before making any calculations (express the answer as an equation). Decide, for example, which observer sees time dilated or length contracted before working with the equations or using them to carry out the calculation. If you have thought about who sees what, who is moving with the event being observed, who sees proper time, and so on, you will find it much easier to determine if your calculation is reasonable.
• Determine the primary type of calculation to be done to find the unknowns identified above (do the calculation). You will find the section summary helpful in determining whether a length contraction, relativistic kinetic energy, or some other concept is involved.

Note that you should not round off during the calculation . As noted in the text, you must often perform your calculations to many digits to see the desired effect. You may round off at the very end of the problem solution, but do not use a rounded number in a subsequent calculation. Also, check the answer to see if it is reasonable: Does it make sense? This may be more difficult for relativity, which has few everyday examples to provide experience with what is reasonable. But you can look for velocities greater than c or relativistic effects that are in the wrong direction (such as a time contraction where a dilation was expected).

Example \(\PageIndex{1A}\): Time Dilation in a High-Speed Vehicle

The Hypersonic Technology Vehicle 2 (HTV-2) is an experimental rocket vehicle capable of traveling at 21,000 km/h (5830 m/s). If an electronic clock in the HTV-2 measures a time interval of exactly 1-s duration, what would observers on Earth measure the time interval to be?

Apply the time dilation formula to relate the proper time interval of the signal in HTV-2 to the time interval measured on the ground.

• Identify the knowns: \(\Delta \tau = 1 \, s\); \(v = 5830m/s.\)
• Identify the unknown: \(\Delta t\).

\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

\[\begin{align*} \Delta t &= \dfrac{1 \, s}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times 10^8 m/s}\right)^2}} \\[4pt] &= 1.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-10}s. \end{align*} \nonumber \]

Significance

The very high speed of the HTV-2 is still only 10 -5 times the speed of light. Relativistic effects for the HTV-2 are negligible for almost all purposes, but are not zero.

What Speeds are Relativistic?

How fast must a vehicle travel for 1 second of time measured on a passenger’s watch in the vehicle to differ by 1% for an observer measuring it from the ground outside?

Use the time dilation formula to find v/c for the given ratio of times.

\[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{1.01}. \nonumber \]

• Identify the unknown: v/c .

\[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - v^2/c^2}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - v^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 - \dfrac{v^2}{c^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \end{align*} \nonumber \]

\[\dfrac{v}{c} = \sqrt{1 - (1/1.01)^2} = 0.14. \nonumber \]

The result shows that an object must travel at very roughly 10% of the speed of light for its motion to produce significant relativistic time dilation effects.

Calculating \(\Delta t\) for a Relativistic Event

Suppose a cosmic ray colliding with a nucleus in Earth’s upper atmosphere produces a muon that has a velocity \(v = 0.950c\). The muon then travels at constant velocity and lives 2.20 μs as measured in the muon’s frame of reference. (You can imagine this as the muon’s internal clock.) How long does the muon live as measured by an earthbound observer (Figure \(\PageIndex{2}\))?

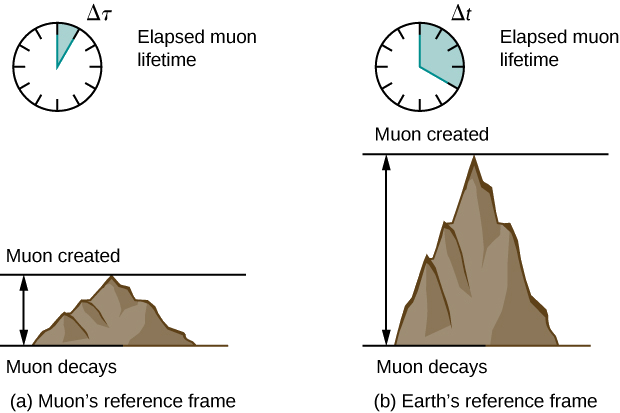
As we will discuss later, in the muon’s reference frame, it travels a shorter distance than measured in Earth’s reference frame.

A clock moving with the muon measures the proper time of its decay process, so the time we are given is \(\Delta \tau = 2.20 \mu s\). The earthbound observer measures \(\Delta t\) as given by the equation \(\Delta t = \gamma \Delta \tau\). Because the velocity is given, we can calculate the time in Earth’s frame of reference.

• Identify the knowns: \(v = 0.950c\); \(\delta \tau = 2.20 \mu s\).

\[\Delta t = \gamma \Delta \tau. \nonumber \]

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

\[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.20 \mu s}{\sqrt{1 - (0.950)^2}} \\[4pt] &= 7.05 \, \mu s.\end{align*} \nonumber \]

One implication of this example is that because \(\gamma = 3.20\) at 95.0% of the speed of light (\(v = 0.950c\)), the relativistic effects are significant. The two time intervals differ by a factor of 3.20, when classically they would be the same. Something moving at 0.950 c is said to be highly relativistic.

Example \(\PageIndex{1B}\): Relativistic Television

A non-flat screen, older-style television display (Figure \(\PageIndex{3}\)) works by accelerating electrons over a short distance to relativistic speed, and then using electromagnetic fields to control where the electron beam strikes a fluorescent layer at the front of the tube. Suppose the electrons travel at \(6.00 \times 10^7 m/s\) through a distance of 0.200m0.200m from the start of the beam to the screen.

• What is the time of travel of an electron in the rest frame of the television set?
• What is the electron’s time of travel in its own rest frame?

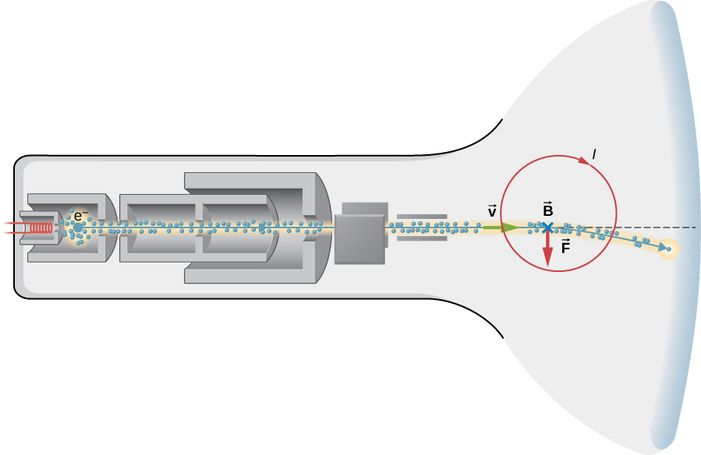
Strategy for (a)

(a) Calculate the time from \(vt = d\). Even though the speed is relativistic, the calculation is entirely in one frame of reference, and relativity is therefore not involved.

\[v = 6.00 \times 10^7 m/s \, d = 0.200 \, m. \nonumber \]

• Identify the unknown: the time of travel \(\Delta t\).

\[\Delta t = \dfrac{d}{v}. \nonumber \]

\[ \begin{align*} t &= \dfrac{0.200 \, m}{6.00 \times 10^7 \, m/s} \\[4pt] &= 3.33 \times 10^{-9} \, s. \end{align*} \nonumber \]

The time of travel is extremely short, as expected. Because the calculation is entirely within a single frame of reference, relativity is not involved, even though the electron speed is close to c .

Strategy for (b)

(b) In the frame of reference of the electron, the vacuum tube is moving and the electron is stationary. The electron-emitting cathode leaves the electron and the front of the vacuum tube strikes the electron with the electron at the same location. Therefore we use the time dilation formula to relate the proper time in the electron rest frame to the time in the television frame.

\[\Delta t = 3.33 \times 10^{-9} \, s; \, v = 6.00 \times 10^7 \, m/s; \, d = 0.200 \, m. \nonumber \]

• Identify the unknown: \(\tau\).

\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - v^2/c^2}}. \nonumber \]

\[\begin{align*} \Delta \tau &= (3.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{3.00 \times 10^8 m/s}\right)^2} \\[4pt] &= 3.26 \times 10^{-9}s. \end{align*} \nonumber \]

The time of travel is shorter in the electron frame of reference. Because the problem requires finding the time interval measured in different reference frames for the same process, relativity is involved. If we had tried to calculate the time in the electron rest frame by simply dividing the 0.200 m by the speed, the result would be slightly incorrect because of the relativistic speed of the electron.

Exercise \(\PageIndex{1}\)

What is \(\gamma\) if \(v = 0.650c\)?

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = 1.32 \nonumber \]

The Twin Paradox

An intriguing consequence of time dilation is that a space traveler moving at a high velocity relative to Earth would age less than the astronaut’s earthbound twin. This is often known as the twin paradox . Imagine the astronaut moving at such a velocity that \(\gamma = 30.0\), as in Figure \(\PageIndex{4}\). A trip that takes 2.00 years in her frame would take 60.0 years in the earthbound twin’s frame. Suppose the astronaut travels 1.00 year to another star system, briefly explores the area, and then travels 1.00 year back. An astronaut who was 40 years old at the start of the trip would be would be 42 when the spaceship returns. Everything on Earth, however, would have aged 60.0 years. The earthbound twin, if still alive, would be 100 years old.

The situation would seem different to the astronaut in Figure \(\PageIndex{4}\). Because motion is relative, the spaceship would seem to be stationary and Earth would appear to move. (This is the sensation you have when flying in a jet.) Looking out the window of the spaceship, the astronaut would see time slow down on Earth by a factor of \(\gamma = 30.0\). Seen from the spaceship, the earthbound sibling will have aged only 2/30, or 0.07, of a year, whereas the astronaut would have aged 2.00 years.

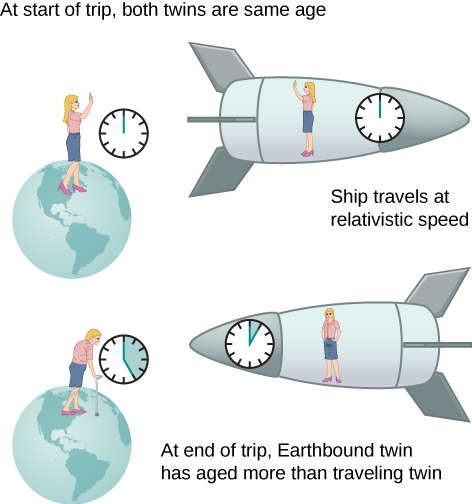
The paradox here is that the two twins cannot both be correct. As with all paradoxes, conflicting conclusions come from a false premise. In fact, the astronaut’s motion is significantly different from that of the earthbound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to Earth, she again accelerates and decelerates. The spacecraft is not in a single inertial frame to which the time dilation formula can be directly applied. That is, the astronaut twin changes inertial references. The earthbound twin does not experience these accelerations and remains in the same inertial frame. Thus, the situation is not symmetric, and it is incorrect to claim that the astronaut observes the same effects as her twin. The lack of symmetry between the twins will be still more evident when we analyze the journey later in this chapter in terms of the path the astronaut follows through four-dimensional space-time.

In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the world on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating’s results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, because gravity and accelerations were involved as well as relative motion.

Exercise \(\PageIndex{2A}\)

a. A particle travels at \(1.90 \times 10^8 \, m/s\) and lives \(2.1 \times 10^8 \, s\) when at rest relative to an observer. How long does the particle live as viewed in the laboratory?

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s. \nonumber \]

Exercise \(\PageIndex{2B}\)

Spacecraft A and B pass in opposite directions at a relative speed of \(4.00 \times 10^7 \, m/s\). An internal clock in spacecraft A causes it to emit a radio signal for 1.00 s. The computer in spacecraft B corrects for the beginning and end of the signal having traveled different distances, to calculate the time interval during which ship A was emitting the signal. What is the time interval that the computer in spacecraft B calculates?

Only the relative speed of the two spacecraft matters because there is no absolute motion through space. The signal is emitted from a fixed location in the frame of reference of A , so the proper time interval of its emission is \(\tau = 1.00 \, s\). The duration of the signal measured from frame of reference B is then

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber \]

• Conversions
• Construction

Calculators » Fun » Travel Time Calculator

Travel Time Calculator

You chose the *Basic version of the Travel Time Calculator.

Create a free account to access the embed code for the Basic version of this calculator!

User information, select additional packages to add to your calculator., lead generation, get this calculator for your site:, travel time formula:, travel time definition.

The Travel Time Calculator will instantly calculate the travel time it takes to get anywhere if you enter the distance to your destination and the average speed you plan to travel. The default units are miles and miles per hour, but the calculator will also work if you use kilometers and kilometers per hour.

If you already know how long it takes (or took) to get to your destination, try our average speed calculator to see what your average speed was.

How to Calculate Travel Time

Let's be honest - sometimes the best travel time calculator is the one that is easy to use and doesn't require us to even know what the travel time formula is in the first place! But if you want to know the exact formula for calculating travel time then please check out the "Formula" box above.

Add a Free Travel Time Calculator Widget to Your Site!

You can get a free online travel time calculator for your website and you don't even have to download the travel time calculator - you can just copy and paste! The travel time calculator exactly as you see it above is 100% free for you to use. If you want to customize the colors, size, and more to better fit your site, then pricing starts at just $29.99 for a one time purchase. Click the "Customize" button above to learn more!

Love our Calculators? Donate to CalculatorPro!

• Privacy Policy

© 2024 Calculator Pro Calculators All Rights Reserved.

Phase naming in TauP

Overview of the comploc package, example of a 1d "layered cake" velocity model, resample the velocity model, compute the travel time table, compute travel time for individual sac traces, usin the layerxt code in shearer (1999) book.

• Docs »
• Seismic »
• Basic principles »
• Travel times
• Edit on GitHub

Travel times ¶

A seismic wave travelling through an isotropic homogeneous medium will propagate at a constant velocity. Therefore, the time \(t\) required for a seismic wave to travel from source to receiver in a homogeneous earth layer with velocity \(v\) is simply given by the formula

where \(d\) is the distance travelled in the layer. In a seismic survey we measure source to receiver travel times and use those data to estimate the properties of the subsurface. Basic seismic interpretation methods assume that the earth is composed of a series of uniform layers and attempt to compute the thicknesses, velocities, and sometimes dips of each layer. We will discuss specific techniques for computing layer thicknesses and velocities in the reflection and refraction survey sections. However, we will introduce the concept of travel time computations and how they relate to geometry here, using the example of a two layered earth.

Consider a layer of thickness h and velocity \(v_1\) overlying a uniform halfspace of velocity \(v_2\) . A source is detonated at time \(t=0\) . We are interested in the waves and arrival times of those waves at a receiver which is located at a distance \(x\) from the source at position \(D\) in the figure below. There are three principal waves that will travel through the earth and arrive at position D. i) direct waves, ii) reflected waves, and iii) critically refracted waves.

The travel time curves for these ray paths are shown below, where the horizontal axis represents distance from the source along the flat surface of the earth, \(x_{crit}\) is called the critical distance, and \(x_{cross}\) the crossover distance. The critical distance is the closest surface point to the source at which the refracted ray can be observed. The crossover distance is the surface point at which the direct and refracted rays arrive at the same time. At offsets from the source greater than the crossover distance the refracted ray will be the first signal to arrive from the source. You can explore these concepts interactively using the Science seismic refraction app . Instructions for using the app can be found here . The following video illustrates the propagation of headwaves and how they relate to the crossover distance

Travel times of visible arrivals are related to the distance between source and receiver ( \(x\) ), thickness of the layer ( \(h\) ) and the wave velocities in the upper layer and basement ( \(v_1\) and \(v_2\) ). Let us denote the arrival times at point \(x\) for the direct, reflected and refracted waves as \(t_{dir}\) , \(t_{refl}\) \(t_{refr}\) respectively. These times are given by the following formulas

Note that the formulas for the direct and refracted waves are linear in \(x\) but that the reflected arrival time formula is not.

Before moving on, let’s look at an example of how travel times show up in the field. The horizontal axis of the following plot shows offset from a seismic receiver. Each line plots the displacement vs time curve of a geophone at a given offset. The plot clearly shows a set of events moving linearly in time from one geophone to the next.

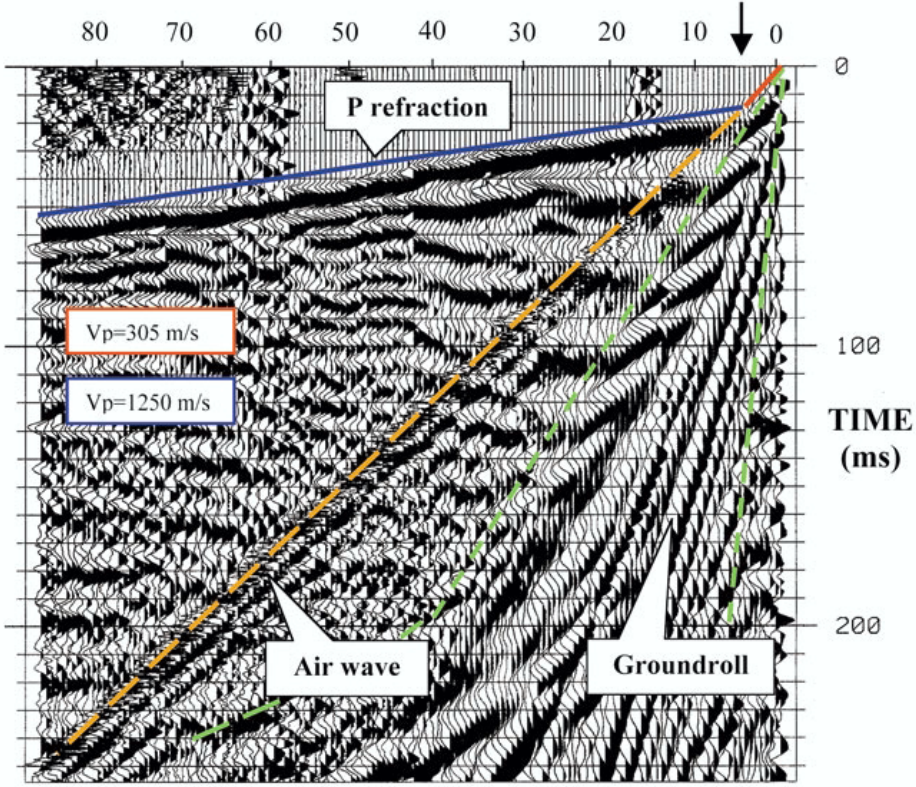
We will now discuss the computation of traveltimes in more detail. It is important to note here that computing traveltimes for an arbitrary, heterogeneous earth is a complex problem well beyond the scope of this course. However, much insight can be gained by assuming that the subsurface consists of a series of homogeneous layers with horizontal or possibly dipping interfaces.

Refracted ray in a two layered-earth ¶

We need to identify specific ray paths and their associated travel times. Consider an earth composed of a uniform layer with velocity \(v_1\) and thickness \(z\) overlying a medium with velocity \(v_2\) . Let \(\theta\) be the critical angle and x denoted the distance between the source at \(A\) and a receiver at \(D\) . Let \(x_c\) denote the critical distance.

From elementary geometry the following relationships hold:

The travel time is the cumulative time for the wave to traverse the path \(ABCD\) . This is \(t=t_{AB}+t_{BC}+t_{CD}\) .

Generally time = distance / velocity, so we can write \(t_{AB} = L/v_1 = (z/cos\theta) / v1\) , (using \(L\) from just above).

Also, we can note that \(t_{AB} = t_{CD}\) and the distance \(BC\) is \(x-x_c\) . So we can now state that \(t=2t_{AB}+t_{BC}\) , or

It is convenient to rearrange this slightly differently. Using the definition for critical angle \(\sin\theta=v_1/v_2\) , we can make the “velocity triangle”, so expressions for the angle arise directly from simple trigonometry:

Use these two relations for \(\cos\) and \(\tan\) in the expression for t above to obtain a useful set of relations.

This simple relation says that the travel time curve is a straight line which has a slope of \(1/v_2\) and an intercept of \(t_i\) . This intercept time is the time where the refraction line extends to intercept the \(y\) -axis –above the source position–. This is not a real “time” - it is derived from the graph.

The velocities of the seismic layers and the layer thickness are obtained in the following manner.

Plot the times of first arrivals on an time-offset plot (“offset” is distance between source and geophone).

The direct arrivals are observed to lie along a straight line joining the origin. The slope of this line is \(1/v_1\) , giving the velocity of the upper layer.

The refracted arrivals appear as a straight line with smaller slope equal to \(1/v_2\) , giving the velocity of the lower layer.

For the refracted wave, this intercept time is

We therefore can obtain all three useful parameters about the earth, \((v_1, z, v_2)\) .

There is another useful point that is observable from the first arrival travel-time plot. We can often discern the crossover distance. Since this is the location where the direct wave and the refracted wave arrive at the same time, we can write

This can be used as a consistency check, or it can be used to compute one of the variables given values for two others.

Refracted ray in a three layered-earth ¶

The extension to more layers is in principle straight forward. Snell’s law holds for waves at all interfaces, so for a multi-layered medium

For a three layer case, the algebra is slightly more involved compared to a two layer example because we need to compute the times due to the ray path segments in the two top layers. Consider the diagrams below:

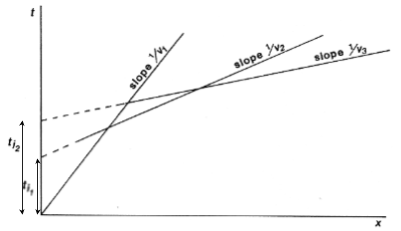
Using arguments that are entirely analagous to the two layer case (above) the travel time for the wave refracted at the top of layer three is given by

All quantities are defined in the diagrams, and the angles are

Note that \(\theta_2\) is a critical angle while \(\theta_1\) is not. You can prove the relation for \(\theta_1\) yourself by using Snell’s law at the two interfaces, and recalling that the angle of the ray coming from point \(B\) is the same as the angle arriving at point \(C\) . The straight line that corresponds to an individual refractor provides a velocity (from its slope) and a thickness (from the intercept). Thus the information on the above travel-time plot allows us to recover all three velocities and the thickness of both layers.

The travel time curves for multi layers are obtained from obvious extension of the above formulation.

Reflected rays - single layer ¶

Consider the situation to the right, in which there is a source \(S\) and a set of receivers on the surface of the earth. The earth is a single uniform layer overlying a uniform halfspace. A reflection from the interface will occur if there is a change in the acoustic impedance at the boundary.

Let \(x\) denote the “offset” or distance from the source to the receiver. The time taken for the seismic energy to travel from the source to the receiver is given by

\[t = \frac{(x^2 + 4z^2)^\frac{1}{2}}{v}\]

This is the equation of a hyperbola. In seismic reflection (as in radar) we plot time on the negative vertical axis, and so the seismic section (without the source wavelet) would look like.

Two way travel time:

Normal Moveout:

In the above diagram \(t_0\) is the 2-way vertical travel time. It is the minimum time at which a reflection will be recorded. The additional time taken for a signal to reach a receiver at offset \(x\) is called the “Normal Moveout” time, \(\Delta t\) . This value is required for every trace in the common depth point data set in order to shift echoes up so they align for stacking. How is it obtained? First let us find a way of determining velocity and \(t_0\) .

For this simple earth structure the velocity and layer thickness can readily be obtained from the hyperbola. Squaring both sides yields,

This is the equation of a straight line when \(t^2\) is plotted against \(x^2\) . Now, to find \(\Delta T\) , we must rearrange this hyperbolic equation relating \(t_0\) , \(x\) , the \(Tx\) – \(Rx\) offset, \(t\) at \(x\) , or \(t(x)\) , and the ground’s velocity, \(v\) .

Apply binomial expansion to get

Now, since normal moveout is \(\Delta T = t_x - t_0\)

The algebra has only one complicated step–a binomial expansion must be applied to obtain a simple relation without square roots etc.

The approximation is valid so long as the source-receiver separation (or offset) is “small” which means much less than the vertical depth to the reflecting layer (i.e. \(x << vt_0\) ). The result is a simple expression for normal moveout.

Each echo can be shifted up to align with the \(t_0\) position, so long as the trace position, \(x\) , the vertical incident travel time, \(t_0\) , and the velocity are known. Velocity can be estimated using the slope of the \(t^2\) – \(x^2\) plot, or with several other methods, which we will discuss in pages following.

Travel Time Curves for Multiple Layers ¶

If there are additional layers then the seismic energy at each interface is refracted according to Snell’s Law. The energy no longer travels in a straight line and hence the travel times are affected. It is observed that for small offsets, the travel time curve is still approximately hyperbolic, but the velocity, which controls the shape of the curve, is an “average” velocity determined from the velocities of all the layers above the reflector. The velocity is called the RMS (Root Mean Square) velocity, \(v_{rms}\) .

The complex travel path of a reflected ray through a multilayered ground. (b) The time–distance curve for reflected rays following the above type of path. Note that the divergence from the hyperbolic travel-time curve for a homogeneous overburden of velocity Vrms increases with offset.

As outlined in the figure above, the reflection curve for small offsets is still like a hyperbola, but the associated velocity is \(v_{rms}\) , not a true interval velocity.

For each hyperbola:

By fitting hyperbolas to each reflection event one can obtain \(t_n,v_n^{rms}\) for n = 1, 2, … The interval velocity and layer thickness of each layer can be found using the formulae below:

These formulae for the interval velocity and thickness of the \(n^{th}\) layer are directly obtainable from the definition of \(v_n^{rms}\) given above. The RMS velocity for the \(n^{th}\) layer is given by:

where \(v_i\) is the velocity of the \(i^{th}\) layer, and \(\tau_i\) is the one-way travel time through the \(i^{th}\) layer.

Giant Freakin Robot

Time Travel Equation Solved By Astrophysicist

Posted: March 25, 2024 | Last updated: March 25, 2024

After a lifetime of pursuing the idea, Physics Professor Ronald Mallett at the University of Connecticut has potentially figured out the theoretical aspects of time travel. Professor Mallett believes that black holes, rotating light, and gravitational pulls may hold the key to exploring time, but it’s all theoretical for now. There are still a lot of hurdles and limitations to handle before time travel can have real, practical applications.

A Life Spent Thinking About Time Travel

Love and loss pushed Professor Mallett into an obsession with time and space. When he was 10 years old, his father passed away from a heart attack. It was his father who nourished his love of science, but H.G. Wells’ book The Time Machine pushed him towards a focus on time travel.

He was hooked from the very first paragraph of the book, “Scientific people know very well that Time is only a kind of Space. And why cannot we move in Time as we move about in the other dimensions of Space?”

That paragraph never left him, and the professor let that time travel question guide him through school and into the Professor Emeritus of Physics position at the University of Connecticut.

Einstein And Black Holes

As he grew up, Professor Mallett spent much of his time on Albert Einstein’s theories about black holes. While his interest in time travel only continued to grow, a potential solution never showed itself. At least, not until the professor ended up in a hospital with a heart condition.

There, lying in the hospital bed, inspiration hit him. Black holes and the gravitational fields they created were the answer to time travel. These gravitational fields had the potential to lead to time loops, which then theoretically could allow people and objects to travel back in time.

Black Holes Manipulating Gravity

While this idea offered an ability to manipulate time, the other problem was how to use these time loops for time travel.

Professor Mallett found this time travel solution much easier than the first problem. Strong and continuous beams of light, like a ring of lasers, with a particular rotation could be used to manipulate gravity and mimic the distorting effects of a black hole.

Though the details are rather complicated, the big time travel picture is a lot simpler to grasp. The professor offers a comparison to help people understand. “Let’s say you have a cup of coffee in front of you. Start stirring the coffee with the spoon. It started to spin, right? That’s what a spinning black hole does. In Einstein’s theory, space and time are related to each other. That’s why it’s called space-time. So when the black hole spins, it will actually cause time to shift.”

Much To Figure Out

Professor Mallett may now have a theory on time travel and a machine to use to make it possible, but that doesn’t mean it will be here in the next few decades.

There’s still a lot to figure out to make such travel practical, such as where the insane amount of energy such a machine would require could come from, and how big the machine would need to be.

There’s also a major constraint on the machine. According to his theories, time travel would only be possible to the very beginning of when the machine was first built. In this way, it’s more like a one-way message service. You can potentially go forward quite a distance, but going back in time is limited by the machine’s creation.

Theoretical Aspects Of Time Travel

The professor has made a huge leap in figuring out the theoretical aspects of time travel, but there’s a lot more to discover and quite a few hurdles and paradoxes to figure out before scientists practically start messing around in time.

Still, the theory is a step in the right direction and does suggest that people can push past what science currently considers possible.

Source: Earth.com

More for You

Russia Issues Furious Warning After Ukraine Aid Bill

3 lies women have been told about their bodies, according to a female doctor

How to 'quiet quit,' from a former teacher who did it for 2 years so she could enjoy a better life while still getting a paycheck

Legal fees pile up for embattled Squad member Cori Bush

Taylor Swift draws backlash for 'all the racists' lyrics on new 'Tortured Poets' album

Study Suggests Possible Link Between CWD and Fatal Human Disease—But with Many Open Questions

I did a single-leg wall sit every day for a week — here's what happened to my legs

Olivia Dunne's LSU gymnastics team wins NCAA title: 'Best day ever'

One of the best British spy dramas of all time is finally streaming on Netflix

If You See Black Residue on Your Cast-Iron Skillet, This Is What It Means

5 people explain what it actually feels like to die

Don't use these 3 types of phrases in your resume, says ex-Google recruiter

This type of supplement may increase heart disease risk, new study finds

I Walked 20k Steps a Day for a Month. The Results Transformed Me

State law takes US a step closer to popular vote deciding presidential elections

How To Identify And Get Rid Of Dangerous Brown Recluse Spiders

19 Things You’re Officially Allowed to Do When You Get Old

15 Succinct Jokes That Really Make You Think

39-year-old left full-time job to grow her side hustle—now she makes $279,000 a year without working 'all the time'

Photo of massive Arrowhead Stadium parking lot raises questions about city design: 'Extraordinarily bad land usage'

An astrophysicist claims he finally figured out time travel

If you buy through a BGR link, we may earn an affiliate commission, helping support our expert product labs.

Time travel has been one of the biggest tropes in science fiction for years. But what if you could actually go back in time and visit a loved one before their death? There’s, obviously, a lot we don’t know about what kind of consequences time travel might bring to the table , but that hasn’t stopped physicist Ron Mallet from a lifelong obsession with trying to figure out the time travel equation.

What’s even more impressive about this lifelong endeavor, though, is that Mallet now claims to have solved the equation and figured out how to build an actual time machine. Mallet’s inspiration and obsession with time travel originally began when he was much younger, Earth.com notes . Following the death of his beloved father, Mallet lost himself in novels, including The Time Machine by H.G. Wells.

It is certainly a respectable goal, especially for anyone who has lost someone they loved dearly. Mallet says that his idea of a time machine centers around an “intense and continuous rotating beam of light” that can manipulate gravity. A device built by him, following his equation, would use a ring of lasers to mimic the effects of a black hole, which appears to distort space and time around them.

Tech. Entertainment. Science. Your inbox.

Sign up for the most interesting tech & entertainment news out there.

By signing up, I agree to the Terms of Use and have reviewed the Privacy Notice.

Of course, learning the time travel equation and building a working time machine are two different things altogether. Sure, scientists have simulated black holes in a lab once or twice, but never anything with the kind of power or reality-effecting pull that Mallet seems to think would make time travel possible. That isn’t to say that he’s got things wrong, though.

His equation for time travel may be exactly what is needed to break through this lifelong obsession and actually travel back in time. But building something capable of testing it is going to be a whole separate endeavor in and of itself.

This article talks about:

Josh Hawkins has been writing for over a decade, covering science, gaming, and tech culture. He also is a top-rated product reviewer with experience in extensively researched product comparisons, headphones, and gaming devices.

Whenever he isn’t busy writing about tech or gadgets, he can usually be found enjoying a new world in a video game, or tinkering with something on his computer.

• This insane home security camera blasts intruders with paintballs
• Groundbreaking hydrogel can remove microplastics from water
• This is your last chance to see the 'devil comet' until 2095

More Science

Uranus is even more mysterious than we thought

Astronomers uncover the heaviest black hole in our galaxy and it’s in our cosmic backyard

NASA struggling to find new plan to make Mars Sample Return work

ISS space junk crashed into a man’s house in Florida, sparking more concerns over space junk

Latest news.

It feels like every major digital service I use is now part of Taylor Swift’s marketing machine

5 post-apocalyptic shows to stream after you finish Fallout

Next year’s iPhone 16 rivals might feature huge batteries – here’s why that might be a problem

The 2 iOS 18 AI features I want the most from the Notes app

Sign up for the most interesting tech & entertainment news out there.