standing vs travelling wave

• TPC and eLearning
• Read Watch Interact
• What's NEW at TPC?
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Traveling Waves vs. Standing Waves
• Formation of Standing Waves
• Nodes and Anti-nodes
• Harmonics and Patterns
• Mathematics of Standing Waves

What is a Standing Wave Pattern?

It is however possible to have a wave confined to a given space in a medium and still produce a regular wave pattern that is readily discernible amidst the motion of the medium. For instance, if an elastic rope is held end-to-end and vibrated at just the right frequency , a wave pattern would be produced that assumes the shape of a sine wave and is seen to change over time. The wave pattern is only produced when one end of the rope is vibrated at just the right frequency. When the proper frequency is used, the interference of the incident wave and the reflected wave occur in such a manner that there are specific points along the medium that appear to be standing still. Because the observed wave pattern is characterized by points that appear to be standing still, the pattern is often called a standing wave pattern . There are other points along the medium whose displacement changes over time, but in a regular manner. These points vibrate back and forth from a positive displacement to a negative displacement; the vibrations occur at regular time intervals such that the motion of the medium is regular and repeating. A pattern is readily observable.

We Would Like to Suggest ...

Standing Waves

Introduction.

Maybe you've noticed or maybe you haven't. Sometimes when you vibrate a string, or cord, or chain, or cable it's possible to get it to vibrate in a manner such that you're generating a wave, but the wave doesn't propagate. It just sits there vibrating up and down in place. Such a wave is called a standing wave and must be seen to be appreciated.

I first discovered standing waves (or I first remember seeing them) while playing around with a phone cord. If you shake the phone cord in just the right manner it's possible to make a wave that appears to stand still. If you shake the phone cord in any other way you'll get a wave that behaves like all the other waves described in this chapter; waves that propagate — traveling waves . Traveling waves have high points called crests and low points called troughs (in the transverse case) or compressed points called compressions and stretched points called rarefactions (in the longitudinal case) that travel through the medium. Standing waves don't go anywhere, but they do have regions where the disturbance of the wave is quite small, almost zero. These locations are called nodes . There are also regions where the disturbance is quite intense, greater than anywhere else in the medium, called antinodes .

Standing waves can form under a variety of conditions, but they are easily demonstrated in a medium which is finite or bounded. A phone cord begins at the base and ends at the handset. (Or is it the other way around?) Other simple examples of finite media are a guitar string (it runs from fret to bridge), a drum head (it's bounded by the rim), the air in a room (it's bounded by the walls), the water in Lake Michigan (it's bounded by the shores), or the surface of the Earth (although not bounded, the surface of the Earth is finite). In general, standing waves can be produced by any two identical waves traveling in opposite directions that have the right wavelength. In a bounded medium, standing waves occur when a wave with the correct wavelength meets its reflection. The interference of these two waves produces a resultant wave that does not appear to move.

Standing waves don't form under just any circumstances. They require that energy be fed into a system at an appropriate frequency. That is, when the driving frequency applied to a system equals its natural frequency . This condition is known as resonance . Standing waves are always associated with resonance. Resonance can be identified by a dramatic increase in amplitude of the resultant vibrations. Compared to traveling waves with the same amplitude, producing standing waves is relatively effortless. In the case of the telephone cord, small motions in the hand result will result in much larger motions of the telephone cord.

Any system in which standing waves can form has numerous natural frequencies. The set of all possible standing waves are known as the harmonics of a system. The simplest of the harmonics is called the fundamental or first harmonic. Subsequent standing waves are called the second harmonic, third harmonic, etc. The harmonics above the fundamental, especially in music theory, are sometimes also called overtones . What wavelengths will form standing waves in a simple, one-dimensional system? There are three simple cases.

one dimension: two fixed ends

If a medium is bounded such that its opposite ends can be considered fixed, nodes will then be found at the ends. The simplest standing wave that can form under these circumstances has one antinode in the middle. This is half a wavelength. To make the next possible standing wave, place a node in the center. We now have one whole wavelength. To make the third possible standing wave, divide the length into thirds by adding another node. This gives us one and a half wavelengths. It should become obvious that to continue all that is needed is to keep adding nodes, dividing the medium into fourths, then fifths, sixths, etc. There are an infinite number of harmonics for this system, but no matter how many times we divide the medium up, we always get a whole number of half wavelengths ( 1 2 λ, 2 2 λ, 3 2 λ, …, n 2 λ).

There are important relations among the harmonics themselves in this sequence. The wavelengths of the harmonics are simple fractions of the fundamental wavelength. If the fundamental wavelength were 1 m the wavelength of the second harmonic would be 1 2  m, the third harmonic would be 1 3  m, the fourth 1 4  m, and so on. Since frequency is inversely proportional to wavelength, the frequencies are also related. The frequencies of the harmonics are whole-number multiples of the fundamental frequency. If the fundamental frequency were 1 Hz the frequency of the second harmonic would be 2 Hz, the third harmonic would be 3 Hz, the fourth 4 Hz, and so on.

one dimension: two free ends

If a medium is bounded such that its opposite ends can be considered free, antinodes will then be found at the ends. The simplest standing wave that can form under these circumstances has one node in the middle. This is half a wavelength. To make the next possible standing wave, place another antinode in the center. We now have one whole wavelength. To make the third possible standing wave, divide the length into thirds by adding another antinode. This gives us one and a half wavelengths. It should become obvious that we will get the same relationships for the standing waves formed between two free ends that we have for two fixed ends. The only difference is that the nodes have been replaced with antinodes and vice versa. Thus when standing waves form in a linear medium that has two free ends a whole number of half wavelengths fit inside the medium and the overtones are whole number multiples of the fundamental frequency

one dimension: one fixed end — one free end

When the medium has one fixed end and one free end the situation changes in an interesting way. A node will always form at the fixed end while an antinode will always form at the free end. The simplest standing wave that can form under these circumstances is one-quarter wavelength long. To make the next possible standing wave add both a node and an antinode, dividing the drawing up into thirds. We now have three-quarters of a wavelength. Repeating this procedure we get five-quarters of a wavelength, then seven-quarters, etc. In this arrangement, there are always an odd number of quarter wavelengths present. Thus the wavelengths of the harmonics are always fractional multiples of the fundamental wavelength with an odd number in the denominator. Likewise, the frequencies of the harmonics are always odd multiples of the fundamental frequency.

The three cases above show that, although not all frequencies will result in standing waves, a simple, one-dimensional system possesses an infinite number of natural frequencies that will. It also shows that these frequencies are simple multiples of some fundamental frequency. For any real-world system, however, the higher frequency standing waves are difficult if not impossible to produce. Tuning forks, for example, vibrate strongly at the fundamental frequency, very little at the second harmonic, and effectively not at all at the higher harmonics.

The best part of a standing wave is not that it appears to stand still, but that the amplitude of a standing wave is much larger that the amplitude of the disturbance driving it. It seems like getting something for nothing. Put a little bit of energy in at the right rate and watch it accumulate into something with a lot of energy. This ability to amplify a wave of one particular frequency over those of any other frequency has numerous applications.

• Basically, all non-digital musical instruments work directly on this principle. What gets put into a musical instrument is vibrations or waves covering a spread of frequencies (for brass, it's the buzzing of the lips; for reeds, it's the raucous squawk of the reed; for percussion, it's the relatively indiscriminate pounding; for strings, it's plucking or scraping; for flutes and organ pipes, it's blowing induced turbulence). What gets amplified is the fundamental frequency plus its multiples. These frequencies are louder than the rest and are heard. All the other frequencies keep their original amplitudes while some are even de-amplified. These other frequencies are quieter in comparison and are not heard.
• You don't need a musical instrument to illustrate this principle. Cup your hands together loosely and hold them next to your ear forming a little chamber. You will notice that one frequency gets amplified out of the background noise in the space around you. Vary the size and shape of this chamber. The amplified pitch changes in response. This is what people hear when the hold a seashell up to their ears. It's not "the ocean" but a few select frequencies amplified out of the noise that always surrounds us.
• During speech, human vocal cords tend to vibrate within a much smaller range that they would while singing. How is it then possible to distinguish the sound of one vowel from another? English is not a tonal language (unlike Chinese and many African languages). There is little difference in the fundamental frequency of the vocal cords for English speakers during a declarative sentence. (Interrogative sentences rise in pitch near the end. Don't they?) Vocal cords don't vibrate with just one frequency, but with all the harmonic frequencies. Different arrangements of the parts of the mouth (teeth, lips, front and back of tongue, etc.) favor different harmonics in a complicated manner. This amplifies some of the frequencies and de-amplifies others. This makes "EE" sound like "EE" and "OO" sound like "OO".
• The filtering effect of resonance is not always useful or beneficial. People that work around machinery are exposed to a variety of frequencies. (This is what noise is.) Due to resonance in the ear canal, sounds near 4,000 Hz are amplified and are thus louder than the other sounds entering the ear. Everyone should know that loud sounds can damage one's hearing. What everyone may not know is that exposure to loud sounds of just one frequency will damage one's hearing at that frequency. People exposed to noise are often experience 4,000 Hz hearing loss. Those afflicted with this condition do not hear sounds near this frequency with the same acuity that unafflicted people do. It is often a precursor to more serious forms of hearing loss.

two dimensions

The type of reasoning used in the discussion so far can also be applied to two-dimensional and three-dimensional systems. As you would expect, the descriptions are a bit more complex. Standing waves in two dimensions have numerous applications in music. A circular drum head is a reasonably simple system on which standing waves can be studied. Instead of having nodes at opposite ends, as was the case for guitar and piano strings, the entire rim of the drum is a node. Other nodes are straight lines and circles. The harmonic frequencies are not simple multiples of the fundamental frequency.

The diagram above shows six simple modes of vibration in a circular drum head. The plus and minus signs show the phase of the antinodes at a particular instant. The numbers follow the (D, C) naming scheme, where D is the number of nodal diameters and C is the number of nodal circumferences.

Standing waves in two dimensions have been applied extensively to the study of violin bodies. Violins manufactured by the Italian violin maker Antonio Stradivari (1644–1737) are renowned for their clarity of tone over a wide dynamic range. Acoustic physicists have been working on reproducing violins equal in quality to those produced by Stradivarius for quite some time. One technique developed by the German physicist Ernst Chladni (1756–1794) involves spreading grains of fine sand on a plate from a dismantled violin that is then clamped and set vibrating with a bow. The sand grains bounce away from the lively antinodes and accumulate at the quiet nodes. The resulting Chladni patterns from different violins could then be compared. Presumably, the patterns from better sounding violins would be similar in some way. Through trial and error, a violin designer should be able to produce components whose behavior mimicked those of the legendary master. This is, of course, just one factor in the design of a violin.

three dimensions

In the one-dimensional case the nodes were points (zero-dimensional). In the two-dimensional case the nodes were curves (one-dimensional). The dimension of the nodes is always one less than the dimension of the system. Thus, in a three-dimensional system the nodes would be two-dimensional surfaces. The most important example of standing waves in three dimensions are the orbitals of an electron in an atom. On the atomic scale, it is usually more appropriate to describe the electron as a wave than as a particle. The square of an electron's wave equation gives the probability function for locating the electron in any particular region. The orbitals used by chemists describe the shape of the region where there is a high probability of finding a particular electron. Electrons are confined to the space surrounding a nucleus in much the same manner that the waves in a guitar string are constrained within the string. The constraint of a string in a guitar forces the string to vibrate with specific frequencies. Likewise, an electron can only vibrate with specific frequencies. In the case of an electron, these frequencies are called eigenfrequencies and the states associated with these frequencies are called eigenstates or eigenfunctions . The set of all eigenfunctions for an electron form a mathematical set called the spherical harmonics . There are an infinite number of these spherical harmonics, but they are specific and discrete . That is, there are no in-between states. Thus an atomic electron can only absorb and emit energy in specific in small packets called quanta . It does this by making a quantum leap from one eigenstate to another. This term has been perverted in popular culture to mean any sudden, large change. In physics, quite the opposite is true. A quantum leap is the smallest possible change of system, not the largest.

mathematics

In mathematics, the infinite sequence of fractions 1 1 , 1 2 , 1 3 , 1 4 , … is called the harmonic sequence . Surprisingly, there are exactly the same number of harmonics described by the harmonic sequence as there are harmonics described by the "odds only" sequence: 1 1 , 1 3 , 1 5 , 1 7 , …. "What? Obviously there are more numbers in the harmonic sequence than there are in the 'odds only' sequence." Nope. There are exactly the same number. Here's the proof. I can set up a one-to-one correspondence between the whole numbers and the odd numbers. Observe. (I will have to play with the format of the numbers to get them to line up correctly on a computer screen, however.)

0 1, 0 2, 0 3, 0 4, 0 5, 0 6, 0 7, 0 8, 0 9, … 0 1, 0 3, 0 5, 0 7, 0 9, 11, 13, 15, 17, …

This can go on forever. Which means there are exactly the same number of odd numbers as there are whole numbers. Both the whole numbers and the odd numbers are examples of countable infinite sets.

There are an infinite number of possible wavelengths that can form standing waves under all of the circumstances described above, but there are an even greater number of wavelengths that can't form standing waves. "What? How can you have more than an infinite amount of something?" Well I don't want to prove that right now so you'll have to trust me, but there are more real numbers between 0 and 1 than there are whole numbers between zero and infinity. Not only do we have all the rational numbers less than one ( 1 2 , 3 5 , 733 2741 , etc.) we also have all the possible algebraic numbers (√2, 7 − √13, etc.) and the whole host of bizarre transcendental numbers (π, e, e π , Feigenbaum's number, etc.). All of these numbers together form an uncountable infinite set called the real numbers . The number of whole numbers is an infinity called aleph null ( ℵ 0 ) the number of real numbers is an infinity called c (for continuum ). The study of infinitely large numbers is known as transfinite mathematics . In this field, it is possible to prove that ℵ 0 is less than c . There is no one-to-one correspondence between the real numbers and the whole numbers. Thus, there are more frequencies that won't form standing waves than there are frequencies that will form standing waves.

Isaac Physics

You need to enable JavaScript to access Isaac Physics.

16.1 Traveling Waves

Learning objectives.

By the end of this section, you will be able to:

• Describe the basic characteristics of wave motion
• Define the terms wavelength, amplitude, period, frequency, and wave speed
• Explain the difference between longitudinal and transverse waves, and give examples of each type
• List the different types of waves

We saw in Oscillations that oscillatory motion is an important type of behavior that can be used to model a wide range of physical phenomena. Oscillatory motion is also important because oscillations can generate waves, which are of fundamental importance in physics. Many of the terms and equations we studied in the chapter on oscillations apply equally well to wave motion ( Figure 16.2 ).

Types of Waves

A wave is a disturbance that propagates, or moves from the place it was created. There are three basic types of waves: mechanical waves, electromagnetic waves, and matter waves.

Basic mechanical wave s are governed by Newton’s laws and require a medium. A medium is the substance mechanical waves propagate through, and the medium produces an elastic restoring force when it is deformed. Mechanical waves transfer energy and momentum, without transferring mass. Some examples of mechanical waves are water waves, sound waves, and seismic waves. The medium for water waves is water; for sound waves, the medium is usually air. (Sound waves can travel in other media as well; we will look at that in more detail in Sound .) For surface water waves, the disturbance occurs on the surface of the water, perhaps created by a rock thrown into a pond or by a swimmer splashing the surface repeatedly. For sound waves, the disturbance is a change in air pressure, perhaps created by the oscillating cone inside a speaker or a vibrating tuning fork. In both cases, the disturbance is the oscillation of the molecules of the fluid. In mechanical waves, energy and momentum transfer with the motion of the wave, whereas the mass oscillates around an equilibrium point. (We discuss this in Energy and Power of a Wave .) Earthquakes generate seismic waves from several types of disturbances, including the disturbance of Earth’s surface and pressure disturbances under the surface. Seismic waves travel through the solids and liquids that form Earth. In this chapter, we focus on mechanical waves.

Electromagnetic waves are associated with oscillations in electric and magnetic fields and do not require a medium. Examples include gamma rays, X-rays, ultraviolet waves, visible light, infrared waves, microwaves, and radio waves. Electromagnetic waves can travel through a vacuum at the speed of light, v = c = 2.99792458 × 10 8 m/s . v = c = 2.99792458 × 10 8 m/s . For example, light from distant stars travels through the vacuum of space and reaches Earth. Electromagnetic waves have some characteristics that are similar to mechanical waves; they are covered in more detail in Electromagnetic Waves .

Matter waves are a central part of the branch of physics known as quantum mechanics. These waves are associated with protons, electrons, neutrons, and other fundamental particles found in nature. The theory that all types of matter have wave-like properties was first proposed by Louis de Broglie in 1924. Matter waves are discussed in Photons and Matter Waves .

Mechanical Waves

Mechanical waves exhibit characteristics common to all waves, such as amplitude, wavelength, period, frequency, and energy. All wave characteristics can be described by a small set of underlying principles.

The simplest mechanical waves repeat themselves for several cycles and are associated with simple harmonic motion. These simple harmonic waves can be modeled using some combination of sine and cosine functions. For example, consider the simplified surface water wave that moves across the surface of water as illustrated in Figure 16.3 . Unlike complex ocean waves, in surface water waves, the medium, in this case water, moves vertically, oscillating up and down, whereas the disturbance of the wave moves horizontally through the medium. In Figure 16.3 , the waves causes a seagull to move up and down in simple harmonic motion as the wave crests and troughs (peaks and valleys) pass under the bird. The crest is the highest point of the wave, and the trough is the lowest part of the wave. The time for one complete oscillation of the up-and-down motion is the wave’s period T . The wave’s frequency is the number of waves that pass through a point per unit time and is equal to f = 1 / T . f = 1 / T . The period can be expressed using any convenient unit of time but is usually measured in seconds; frequency is usually measured in hertz (Hz), where 1 Hz = 1 s −1 . 1 Hz = 1 s −1 .

The length of the wave is called the wavelength and is represented by the Greek letter lambda ( λ ) ( λ ) , which is measured in any convenient unit of length, such as a centimeter or meter. The wavelength can be measured between any two similar points along the medium that have the same height and the same slope. In Figure 16.3 , the wavelength is shown measured between two crests. As stated above, the period of the wave is equal to the time for one oscillation, but it is also equal to the time for one wavelength to pass through a point along the wave’s path.

The amplitude of the wave ( A ) is a measure of the maximum displacement of the medium from its equilibrium position. In the figure, the equilibrium position is indicated by the dotted line, which is the height of the water if there were no waves moving through it. In this case, the wave is symmetrical, the crest of the wave is a distance + A + A above the equilibrium position, and the trough is a distance − A − A below the equilibrium position. The units for the amplitude can be centimeters or meters, or any convenient unit of distance.

The water wave in the figure moves through the medium with a propagation velocity v → . v → . The magnitude of the wave velocity is the distance the wave travels in a given time, which is one wavelength in the time of one period, and the wave speed is the magnitude of wave velocity. In equation form, this is

This fundamental relationship holds for all types of waves. For water waves, v is the speed of a surface wave; for sound, v is the speed of sound; and for visible light, v is the speed of light.

Transverse and Longitudinal Waves

We have seen that a simple mechanical wave consists of a periodic disturbance that propagates from one place to another through a medium. In Figure 16.4 (a), the wave propagates in the horizontal direction, whereas the medium is disturbed in the vertical direction. Such a wave is called a transverse wave . In a transverse wave, the wave may propagate in any direction, but the disturbance of the medium is perpendicular to the direction of propagation. In contrast, in a longitudinal wave or compressional wave, the disturbance is parallel to the direction of propagation. Figure 16.4 (b) shows an example of a longitudinal wave. The size of the disturbance is its amplitude A and is completely independent of the speed of propagation v .

A simple graphical representation of a section of the spring shown in Figure 16.4 (b) is shown in Figure 16.5 . Figure 16.5 (a) shows the equilibrium position of the spring before any waves move down it. A point on the spring is marked with a blue dot. Figure 16.5 (b) through (g) show snapshots of the spring taken one-quarter of a period apart, sometime after the end of` the spring is oscillated back and forth in the x -direction at a constant frequency. The disturbance of the wave is seen as the compressions and the expansions of the spring. Note that the blue dot oscillates around its equilibrium position a distance A , as the longitudinal wave moves in the positive x -direction with a constant speed. The distance A is the amplitude of the wave. The y -position of the dot does not change as the wave moves through the spring. The wavelength of the wave is measured in part (d). The wavelength depends on the speed of the wave and the frequency of the driving force.

Waves may be transverse, longitudinal, or a combination of the two. Examples of transverse waves are the waves on stringed instruments or surface waves on water, such as ripples moving on a pond. Sound waves in air and water are longitudinal. With sound waves, the disturbances are periodic variations in pressure that are transmitted in fluids. Fluids do not have appreciable shear strength, and for this reason, the sound waves in them are longitudinal waves. Sound in solids can have both longitudinal and transverse components, such as those in a seismic wave. Earthquakes generate seismic waves under Earth’s surface with both longitudinal and transverse components (called compressional or P-waves and shear or S-waves, respectively). The components of seismic waves have important individual characteristics—they propagate at different speeds, for example. Earthquakes also have surface waves that are similar to surface waves on water. Ocean waves also have both transverse and longitudinal components.

Example 16.1

Wave on a string.

• The speed of the wave can be derived by dividing the distance traveled by the time.
• The period of the wave is the inverse of the frequency of the driving force.
• The wavelength can be found from the speed and the period v = λ / T . v = λ / T .
• The first wave traveled 30.00 m in 6.00 s: v = 30.00 m 6.00 s = 5.00 m s . v = 30.00 m 6.00 s = 5.00 m s .
• The period is equal to the inverse of the frequency: T = 1 f = 1 2.00 s −1 = 0.50 s . T = 1 f = 1 2.00 s −1 = 0.50 s .
• The wavelength is equal to the velocity times the period: λ = v T = 5.00 m s ( 0.50 s ) = 2.50 m . λ = v T = 5.00 m s ( 0.50 s ) = 2.50 m .

Significance

Check your understanding 16.1.

When a guitar string is plucked, the guitar string oscillates as a result of waves moving through the string. The vibrations of the string cause the air molecules to oscillate, forming sound waves. The frequency of the sound waves is equal to the frequency of the vibrating string. Is the wavelength of the sound wave always equal to the wavelength of the waves on the string?

Example 16.2

Characteristics of a wave.

• The amplitude and wavelength can be determined from the graph.
• Since the velocity is constant, the velocity of the wave can be found by dividing the distance traveled by the wave by the time it took the wave to travel the distance.
• The period can be found from v = λ T v = λ T and the frequency from f = 1 T . f = 1 T .
• The distance the wave traveled from time t = 0.00 s t = 0.00 s to time t = 3.00 s t = 3.00 s can be seen in the graph. Consider the red arrow, which shows the distance the crest has moved in 3 s. The distance is 8.00 cm − 2.00 cm = 6.00 cm . 8.00 cm − 2.00 cm = 6.00 cm . The velocity is v = Δ x Δ t = 8.00 cm − 2.00 cm 3.00 s − 0.00 s = 2.00 cm/s . v = Δ x Δ t = 8.00 cm − 2.00 cm 3.00 s − 0.00 s = 2.00 cm/s .
• The period is T = λ v = 8.00 cm 2.00 cm/s = 4.00 s T = λ v = 8.00 cm 2.00 cm/s = 4.00 s and the frequency is f = 1 T = 1 4.00 s = 0.25 Hz . f = 1 T = 1 4.00 s = 0.25 Hz .

Check Your Understanding 16.2

The propagation velocity of a transverse or longitudinal mechanical wave may be constant as the wave disturbance moves through the medium. Consider a transverse mechanical wave: Is the velocity of the medium also constant?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/16-1-traveling-waves

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Study Guide 1 - Standing and Travelling Waves

Evaluate each of the following: 

Check your answer

The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\) to give \(121.47^\circ\) \(-0.522\)

The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\) to give \(102^\circ\) \(0.978\)

The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\) \(0.0483\)

Notice that the sine and the angle in radians are equal for small angles, so if you had recognized this at the beginning then the answer could be written down without any calculation.  This is known as the small angle approximation.

Can a sine or cosine ever be greater than 1?

No! So there is no possible answer.

Let \(\mathrm {2\gamma -2 = \theta}\) Then \(\sin \theta = 0.444\)

Now find \(\theta\):

\(\mathrm {\theta = 26.4^\circ or\; 0.460 \;rad}\)

Using the CAST rule \(\theta\) also equals \(\mathrm {180 - 26.4 =153.6^\circ\; or \;2.68\; rad.}\) Now we see that the quantity \(2\gamma -2\) has two solutions. Do we use the degree or the radian answers?

We must use the radian value since the 2 in \(2\gamma -2\) is also in radians.

Solution 1 \(\mathrm {2\gamma - 2 = 0.460\;rad}\) \(\mathrm {\gamma = 1.23 \;rad\; or \;70.5^\circ}\)

Solution 2 \(\mathrm {2\gamma - 2 = 2.68\; rad}\) \(\mathrm {\gamma = 2.34\;rad \;or \;134^\circ}\)

This is a positive sine curve with a repeat distance of 2.0 s (the period is 2.0 s) and an amplitude of 0.1 m. Therefore,

A wave (SI units) has the equation \(y = 4 \sin (3\pi t - 6\pi x)\)

(a) Is the wave travelling in the \(+x\)- or \(- x\) -direction?  

Check your answers

(a) If the time is increased by a small amount, say \(\Delta t\), does \(x\) have to increase by a small amount \(\Delta x\) or decrease to keep \(y\) constant? Answer \(\Delta x\) must increase so that \([3\pi (t+\Delta t) - 6\pi (x+\Delta x)]\) is unchanged, i.e., the wave moves in the \(+x\) -direction.

(b) What are the: amplitude, period, wavelength,wave-vector, frequency, angular frequency (all with SI units)?  

(b) Compare with the standard form \(y = A \sin (\omega t - kx)\) where the angular frequency is defined as \(\omega = 2\pi f = \frac{2\pi}{T}\) and the wave vector is defined as \(k = \frac{2\pi}{\lambda}\) . Answer Amplitude: \(A = 4 \; \mathrm{m}\) Wave vector: \( k = 6 \pi \; \mathrm{m}^{-1}= \frac{2 \pi}{\lambda}\)

Therefore Wavelength: \(\lambda = 1/3\; \mathrm{m}\)

Angular frequency: \(\omega = 3\pi \; \mathrm {rad/s}\)

Frequency: \(f = \frac{\omega}{2\pi} = 3/2 \;\mathrm {Hz}\)

Period: \(T = 1/f = 2/3 \; \mathrm {s}\)

(c) Sketch the graph of this wave at \(t = 0.900 \; \mathrm{s}\).  

\(y = 4 \sin [(3\pi \mathrm{s}^{-1})( 0.900 \; \mathrm{s}) - (6 \pi \; \mathrm{m}^{-1}) x]\)

Find the places where \(y = 0\), i.e.,

\(y = 0 \; \mathrm{when} \; \sin [(3\pi \; \mathrm{s}^{-1})( 0.900 \; \mathrm{s}) - (6 \pi \; \mathrm{m}^{-1}) x] = 0\).

This requires that

\( 2.7\pi - (6 \pi \; \mathrm{m}^{-1}) x = 0\) \(\therefore x = 2.7/6 = 0.450 \; \mathrm{m}\) Of course \(y\) is also 0 at every wavelength multiple (1/3 m see part b, above) on either side of this point, i.e., \(0.450 \; \mathrm{m} - 0.333 \; \mathrm{m} = 0.117 \; \mathrm{m}\) \(0.450 \; \mathrm{m} - 2(0.333 \; \mathrm{m}) = -0.216 \; \mathrm{m}\)

Is \(y\) increasing or decreasing as \(x\) increases by \(\Delta x\) at these points?

Add \(\Delta x\) to \(x\): \(2.7 \pi - 6 \pi (x + \Delta x)\)

decreases because of the negative sign.  Therefore, \(\sin[2.7\pi - 6\pi (x + \Delta x)]\) decreases and therefore \(y\) decreases.

Half way between these points the curve is going the other way.

Final graph:

(d) Sketch the graph of the displacement vs. time at a position \(\mathrm {x = 0.400 \;m.}\)  

\(\mathrm {At \;x = 0.400}\) \(\mathrm {y = 4 \sin[3\pi t - 6\pi (0.4)] = 4 \sin(3\pi t - 2.4\pi)}\) \(\mathrm {Find\;the \;places \;where\; y = 0}\)

\(\mathrm {y = 0 \;when\; \sin (3\pi t - 2.4\pi ) = 0}\) \(\mathrm {i.e., \;when\; 3p\pi t - 2.4\pi = 0}\) \(\mathrm {t = 2.4/3 = 0.8\; s}\) \(\mathrm{Of \;course\; it\; is\; also\; 0 \;every \;T (T = 0.667 \;s, \;see \;part \;b \;above)\; from\; there.}\) \(\mathrm {i.e., 0.8 - 0.667 = 0.133 \;s}\)

Is \(\mathrm {y}\) increasing or decreasing as \(\mathrm{t}\) is increased by \(\mathrm {\Delta \; t}\) at these points?

\(\mathrm{Add\; \Delta \; t\; to\; t}\) \(\mathrm {(3p\pi \;t+\Delta \; t -2.4\pi) \;increases.}\) \(\mathrm {Therefore \;the\; \sin \;increases \;and \;y\; increases.}\)

Half way between these points the curve is going the other way. The complete graph is:

The incident wave in problem 10 and the reflected wave \(\mathrm {y = -4 \sin (3\pi\; t + 6\pi \; x)}\) produce a standing wave.

(a) Write the equation of the standing wave.

\(\mathrm {y = -2A\; \cos\omega \; t \ \sin\;kx}\) \(\mathrm {where: \omega = 3\pi, \;k = 6\pi \;and\; A = 4}\)

Therefore \(\mathrm {y = -8\cos3\pi t\; \sin\; 6\pi \;x}\)

(b) Sketch the standing wave at:

(i) t = 0 s

(ii) t = T/4 s

\(\mathrm {y = -8 \cos3\pi \; t \sin\;6\pi \; x}\)

(iii) t = 3/15 s

An incident wave \(\mathrm {y = -4\sin(3\pi \; t - 6\pi \; x)}\) and a reflected wave \(\mathrm {y = 4 \sin(3\pi\; t + 6\pi \; x)}\) produce a standing wave. What is the equation?  

Remember the standard form: \(\mathrm {y_1 = A \sin(\omega t - kx)}\) \(\mathrm {y_2 = -A \sin(\omega t + kx)}\) Produces: \(\mathrm {y = y_1 + y_2 = -2A\cos \omega t \;\cos\; kx}\)

In this case the amplitudes are reversed in sign but not the direction of the waves so only the sign of the standing wave amplitude is reversed. \(\mathrm {y = 8 \cos \omega t \sin \;kx}\)

A standing wave of equation \(\mathrm {y = -6\cos 6t \sin \;4x}\) is formed from a reflected wave moving in the \(\mathrm {+x}\) direction, and an incident wave moving in the \(\mathrm {-x}\) direction. What are the equations of the incident and reflected waves?

\(\mathrm {y = -6 \cos 6t \sin \;4x}\) \(\mathrm {w = 6, k = 4}\) Reversing the direction of the waves but not the sign of the amplitudes (i.e., incident + and reflected -) would reverse the sign of the standing wave amplitude so it would be \(\mathrm {2 \times 3 = 6.}\) Since the standing wave amplitude is negative, then the signs of the travelling wave amplitudes must also be reversed. \(\mathrm {y_i = -3 \sin (6t + 4x) (+ sign \;means \;to \;the\; -x \;direction)}\) \(\mathrm {y_r = 3 \sin (6t - 4x) (- sign \;means \;to \;the\; +x \;direction)}\)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.8: Travelling and standing wave solutions of the wave equation

• Last updated
• Save as PDF
• Page ID 14009

• Douglas Cline
• University of Rochester

The wave equation can have both travelling and standing-wave solutions. Consider a one-dimensional travelling wave with velocity \(v\) having a specific wavenumber \(k \equiv \frac{2\pi}{\lambda} \). Then the travelling wave is best written in terms of the phase of the wave as

\[ \label{eq:3.97} \Psi(x,t) = A(k)e^{i\frac{2\pi}{\lambda}(x \mp vt)} = A(k)e^{i(kx \mp \omega t)}\]

where the wave number \(k \equiv \frac{2\pi}{\lambda} \), with \(\lambda\) being the wave length, and angular frequency \(\omega \equiv kv \). This particular solution satisfies the wave equation and corresponds to a travelling wave with phase velocity \( v = \frac{\omega_n}{k_n}\) in the positive or negative direction \(x\) depending on whether the sign is negative or positive. Assuming that the superposition principle applies, then the superposition of these two particular solutions of the wave equation can be written as

\[ \label{eq:3.98} \Psi(x,t) = A(k)(e^{i (kx - \omega t)} + e^{i(kx + \omega t)}) = A(k)e^{ikx}(e^{- i \omega t} + e^{i \omega t}) = 2A(k)e^{ikx} \cos \omega t \]

Thus the superposition of two identical single wavelength travelling waves propagating in opposite directions can correspond to a standing wave solution. Note that a standing wave is identical to a stationary normal mode of the system discussed in chapter \(14\). This transformation between standing and travelling waves can be reversed, that is, the superposition of two standing waves, i.e. normal modes, can lead to a travelling wave solution of the wave equation. Discussion of waveforms is simplified when using either of the following two limits.

1) The time dependence of the waveform at a given location \(x = x_0\) which can be expressed using a Fourier decomposition, appendix \(19.9.2\), of the time dependence as a function of angular frequency \( \omega = n\omega_0\).

\[ \label{eq:3.99}\Psi(x_0,t) = \sum_{n= - \infty}^\infty A_n e^{in(k_0x_0-\omega_0t)} = \sum_{n= - \infty}^\infty B_n (x_0)e^{-in\omega_0t}\]

2) The spatial dependence of the waveform at a given instant \(t = t_0\) which can be expressed using a Fourier decomposition of the spatial dependence as a function of wavenumber \( k = nk_0\)

\[ \label{eq:3.100}\Psi(x,t_0) = \sum_{n= - \infty}^\infty A_n e^{in(k_0x-\omega_1t_0)} = \sum_{n= - \infty}^\infty C_n (t_0)e^{ink_0x}\]

The above is applicable both to discrete, or continuous linear oscillator systems, e.g. waves on a string. In summary, stationary normal modes of a system are obtained by a superposition of travelling waves travelling in opposite directions, or equivalently, travelling waves can result from a superposition of stationary normal modes.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• News & Views
• Published: 28 July 2022

FUNCTIONAL CONNECTIVITY

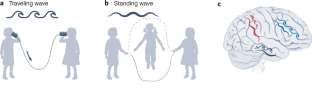
Traveling and standing waves in the brain

• Javier Gonzalez-Castillo   ORCID: orcid.org/0000-0002-6520-5125 1  

Nature Neuroscience volume  25 ,  pages 980–981 ( 2022 ) Cite this article

3963 Accesses

4 Citations

5 Altmetric

Metrics details

• Computational biology and bioinformatics
• Neuroscience

Studying the natural wanderings of the living brain is extremely challenging. Bolt et al. describe a new framework for considering the brain’s intrinsic activity based on the geophysical concepts of standing and traveling waves.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

On-chip phonon-magnon reservoir for neuromorphic computing

• Dmytro D. Yaremkevich
• , Alexey V. Scherbakov
•  …  Manfred Bayer

Nature Communications Open Access 14 December 2023

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 12 print issues and online access

195,33 € per year

only 16,28 € per issue

Rent or buy this article

Prices vary by article type

Prices may be subject to local taxes which are calculated during checkout

Bolt, T. et al. Nat. Neurosci. https://doi.org/10.1038/s41593-022-01118-1 (2022).

Article   PubMed   Google Scholar  

Ogawa, S. et al. Biophys. J. 64 , 803–812 (1993).

Article   CAS   Google Scholar  

Lu, H., Golay, X., Pekar, J. J. & Van Zijl, P. C. M. Magn. Reson. Med. 50 , 263–274 (2003).

Article   Google Scholar  

Caballero-Gaudes, C. & Reynolds, R. C. Neuroimage 154 , 128–149 (2017).

Biswal, B., Yetkin, F. Z., Haughton, V. M. & Hyde, J. S. Magn. Reson. Med. 34 , 537–541 (1995).

Gonzalez-Castillo, J. et al. Neuroimage 202 , 116129 (2019).

Abbas, A. et al. Neuroimage 191 , 193–204 (2019).

Liu, T. T., Nalci, A. & Falahpour, M. Neuroimage 150 , 213–229 (2017).

Liu, X., Zhang, N., Chang, C. & Duyn, J. H. Neuroimage 180 , 485–494 (2018).

Fox, M. D. et al. Proc. Natl Acad. Sci. USA 102 , 9673–9678 (2005).

Margulies, D. S. et al. Proc. Natl Acad. Sci. USA 113 , 12574–12579 (2016).

Smith, S., Miller, K., Moeller, S. & Xu, J. Proc. Natl Acad. Sci. USA 109 , 3131–3136 (2012).

Vidaurre, D., Smith, S. M. & Woolrich, M. W. Proc. Natl Acad. Sci. USA 114 , 12827–12832 (2017).

Gonzalez-Castillo, J., Kam, J. W. Y., Hoy, C. W. & Bandettini, P. A. J. Neurosci. 41 , 1130–1141 (2021).

Download references

Acknowledgements

J.G.-C. was supported by the Intramural Research Program of the National Institute of Mental Health (annual report ZIAMH002783).

Author information

Authors and affiliations.

Section on Functional Imaging Methods, National Institute of Mental Health, National Institutes of Health, Bethesda, MD, USA

Javier Gonzalez-Castillo

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Javier Gonzalez-Castillo .

Ethics declarations

Competing interests.

The author declares no competing interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Gonzalez-Castillo, J. Traveling and standing waves in the brain. Nat Neurosci 25 , 980–981 (2022). https://doi.org/10.1038/s41593-022-01119-0

Download citation

Published : 28 July 2022

Issue Date : August 2022

DOI : https://doi.org/10.1038/s41593-022-01119-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

• Alexey V. Scherbakov
• Manfred Bayer

Nature Communications (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.